轻松掌握：三角形斜边长度计算方法及应用详解

本文系统地讲解了三角形斜边长度的计算方法，涵盖了直角三角形和非直角三角形的计算方法，并结合实际案例分析了勾股定理和三角函数在斜边计算中的应用。文章还展望了斜边计算在未来的发展趋势，相信读者在阅读后能够掌握计算三角形斜边长度的技巧，并在实际生活中灵活运用。

勾股定理：计算直角三角形斜边的基石

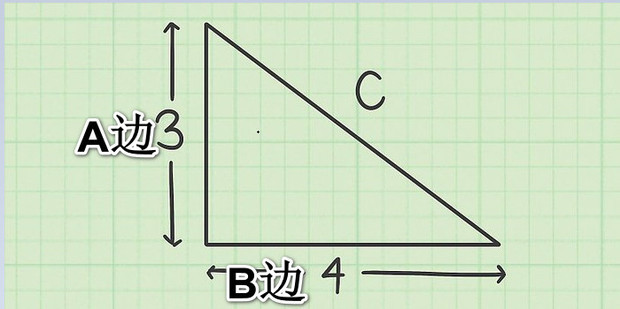
在学习如何计算三角形斜边长度之前，首先需要了解勾股定理。勾股定理是几何学中的一个基本定理，它指出在直角三角形中，两条直角边的平方和等于斜边的平方。用公式表示为：a² + b² = c²，其中a和b分别表示直角三角形的两条直角边长度，c表示斜边长度。

理解勾股定理的关键在于认识到它是一种数学关系，这种关系适用于所有直角三角形。无论是大小，形状如何，只要是直角三角形，这个公式都能完美地计算出斜边的长度。

例如，一个直角三角形的两条直角边分别为3厘米和4厘米，那么根据勾股定理，斜边的长度可以计算为：√(3² + 4²) = √(9 + 16) = √25 = 5厘米。 这个简单的例子清晰地展示了勾股定理在计算直角三角形斜边长度时的应用。

此外，勾股定理不仅仅局限于简单的数值计算，它也是解决很多几何问题的重要工具，例如测量建筑物的高度、计算田地的面积等等。

运用勾股定理解决实际问题：案例分析

勾股定理的应用远不止于书本上的例题，它广泛应用于日常生活和各种工程领域。例如，建筑工人需要计算斜屋顶的长度，就可以运用勾股定理。假设屋顶高度为3米，水平距离为4米，那么屋顶斜边的长度就是√(3² + 4²) = 5米。

另一个例子是测量河流的宽度。假设站在河岸的一侧，沿着河岸方向测量出距离A点10米的B点，再测出A点到对岸树C点的距离为15米，那么我们可以建立一个直角三角形，其中AB为一条直角边(10米)，AC为斜边(15米)。根据勾股定理，我们可以计算出河流的宽度BC为√(15² - 10²) = √125 ≈ 11.18米。

再比如，在导航领域，计算两点之间的距离，若已知经纬度信息，通过坐标转换，可以将问题转化为空间直角坐标系中的距离计算，本质上还是勾股定理在多维空间的拓展。 这些例子充分说明了勾股定理在实际生活中的实用性和重要性，掌握勾股定理能够解决许多实际问题。

非直角三角形斜边长度计算：三角函数的运用

对于非直角三角形，计算斜边长度则需要用到三角函数，主要包括正弦、余弦和正切函数。

假设已知三角形的两条边a和b，以及它们之间的夹角C，那么斜边c的长度可以用余弦定理计算：c² = a² + b² - 2abcosC。

如果已知三角形的一条边和两个角，则可以使用正弦定理来计算斜边长度。正弦定理指出，三角形的任意一边与它所对角的正弦的比值都相等。 具体计算方法需要结合已知条件进行分析和推导。

例如，已知一个三角形两边长分别为 5 和 7，夹角为 60°，则斜边长可以根据余弦定理计算：c² = 5² + 7² - 2*5*7*cos60° = 25 + 49 - 70*(1/2) = 34，所以c = √34。 运用三角函数，可以解决更多类型的三角形斜边计算问题。

斜边计算在不同领域的应用与未来展望

三角形斜边长度的计算方法在诸多领域都有着广泛的应用，从基础的几何测量到复杂的工程设计，都离不开对斜边长度的精确计算。

在建筑工程中，计算屋顶斜坡、桥梁跨度等都需要用到三角形斜边计算；在导航系统中，计算两点间最短距离也依赖于斜边计算；在计算机图形学中，渲染三维模型也需要进行大量的三角形斜边计算。

随着科技的进步，计算方法也在不断完善，例如，一些软件可以使用数值计算方法精确计算复杂形状的斜边长度，极大地提高了效率和精度。未来，随着人工智能和机器学习技术的发展，三角形斜边长度的计算方法可能会更加高效和智能化，例如，利用深度学习技术进行更精准的斜边长度预测，进一步提高工程设计和测量计算的精度和效率，服务于更广阔的应用场景。