本文深入浅出地讲解了梯形的面积计算方法,包括公式推导、不同类型梯形的计算以及在实际生活中的应用。文章强调熟练掌握公式和灵活运用计算技巧的重要性,并展望了未来梯形面积计算技术的发展趋势。学习掌握梯形面积计算,无论是对于学生还是实际工作者,都有着重要的意义,可以帮助解决实际问题,例如计算建筑面积、田地面积等,同时也能提升数学素养。
梯形面积计算公式及推导
梯形的面积计算是几何学中的一个基本问题,其公式简洁明了,但理解其推导过程对于掌握公式的应用至关重要。
最常用的梯形面积计算公式是:S = (a+b)h/2,其中S代表梯形的面积,a和b分别代表梯形的上下底长,h代表梯形的高。
这个公式的推导可以从将梯形分割成已知面积图形入手。我们可以将梯形沿高分成一个矩形和两个直角三角形。矩形的面积为bh,两个直角三角形的面积分别为ah/2和(b-a)h/2 (a 理解这个推导过程,有助于我们更好地理解和运用梯形面积计算公式,尤其是在遇到一些不规则梯形时,我们可以通过分割的方法,将复杂的梯形转换为更容易计算的图形。 例如,一个等腰梯形的面积计算,同样可以使用这个公式。一个上下底分别为 6cm 和 10cm,高为 4cm 的等腰梯形,其面积为:(6+10)*4/2 = 32平方厘米。又例如,一个直角梯形,可以分割成一个矩形和一个三角形来计算,最终结果与公式计算结果一致。 除了标准的梯形面积计算公式外,对于一些特殊类型的梯形,例如等腰梯形和直角梯形,我们可以根据其特殊性质,采用更简便的计算方法。 对于等腰梯形,由于其两腰相等,我们可以通过构造辅助线,将其分割成更容易计算的图形。例如,可以将等腰梯形分割成一个矩形和两个全等的直角三角形,分别计算其面积后相加。也可以利用等腰梯形的对称性,找到对称轴,将梯形分割成两个全等的三角形,然后计算其中一个三角形的面积,再乘以2。 对于直角梯形,我们可以将其分割成一个矩形和一个直角三角形,分别计算面积后相加。或者,可以直接应用梯形面积计算公式,将直角梯形的两底和高代入公式进行计算。 实际应用中,我们常常会遇到各种不同类型的梯形,需要灵活运用不同的计算方法。例如,在土木工程中,计算梯形挡土墙的面积时,工程师需要根据挡土墙的具体形状和尺寸,选择合适的计算方法。而农业生产中,计算梯形田地的面积时,同样需要运用这些知识。 梯形面积的计算并非只是数学课堂上的抽象概念,它广泛应用于许多实际场景中。 在建筑工程中,计算建筑物屋顶、墙面等梯形部分的面积时,需要用到梯形面积计算公式。例如,计算一个斜屋顶的面积,需要将屋顶分解成若干个梯形,分别计算每个梯形的面积,再将所有梯形的面积相加,才能得到屋顶的总面积。 在农业生产中,测量梯形形状田地的面积也是日常工作的一部分。准确计算田地面积有助于合理安排农作物种植,优化资源配置,提高农业生产效率。 此外,在园林绿化、服装设计、工业制造等领域,梯形面积计算也发挥着重要作用。比如,计算不规则花坛面积、设计服装图案、计算机械零件的面积等。 总而言之,理解并掌握梯形面积计算方法,不仅能够解决数学问题,还能帮助我们在实际生活中解决许多实际问题。 本文详细讲解了梯形面积的计算方法,从公式推导、不同类型梯形的计算方法到实际应用,力求全面、系统地阐述这一数学知识点。 在未来的学习和应用中,我们不仅要熟练掌握公式,更要理解其背后的原理,并能灵活运用到各种实际问题中。 同时,随着科技的发展,新的计算工具和方法不断涌现,未来梯形面积的计算可能会更加便捷高效。例如,利用计算机软件或智能手机应用程序,可以快速、准确地计算各种形状梯形的面积。 总而言之,掌握梯形面积的计算方法,具有重要的理论和实践意义,希望本文能够帮助读者更好地理解和应用这一知识。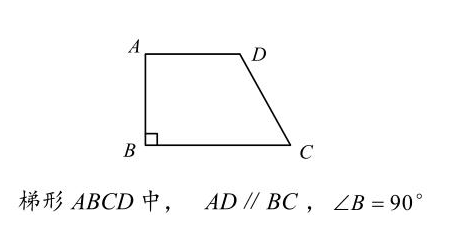
不同类型梯形的面积计算
梯形面积计算在实际生活中的应用
掌握梯形面积计算的技巧和方法
总结与展望

 鄂ICP备15020274号-1
鄂ICP备15020274号-1