圆锥的侧面积怎么求：完全分析与实际应用

霜林尽染 2025-01-01 实时热搜 222 次浏览 0个评论

本文详细解释了圆锥侧面积的计算方法，从基本公式到侧长的求出，再到其在各种领域中的实际应用，并提出了在计算过程中应注意的问题。本文的内容性非常完整，帮助读者完整掌握圆锥侧面积的计算方法。可以为圆锥侧面积计算应用和圆锥侧长的求出进行详细研究。

圆锥侧面积的基本公式与导出

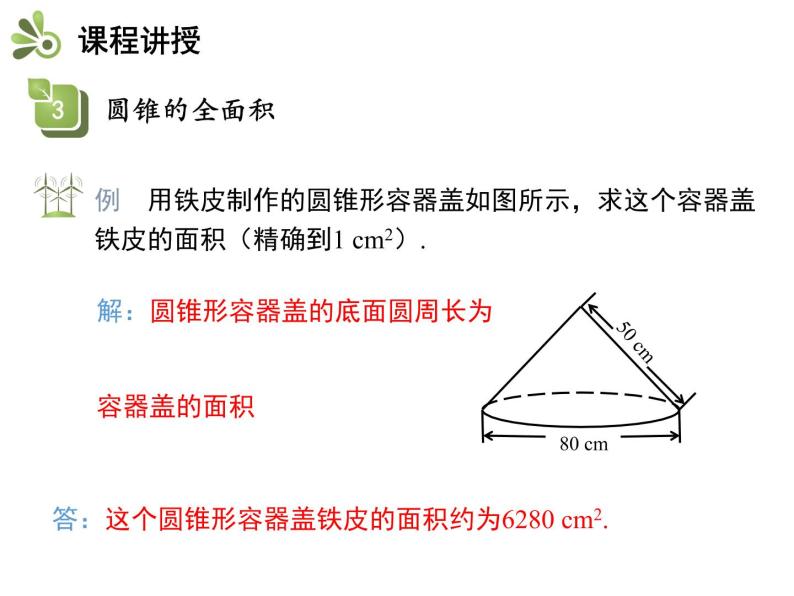
圆锥的侧面积计算是中学数学中一个重要的内容。它的公式为 S = πrl，在此公式中： S 代表圆锥的侧面积；r 代表圆锥的底径；l 代表圆锥的侧长。我们可以把圆锥的侧面看作一个圆片，将其底径作为圆片的半径，侧长作为圆片的轮廓的长度。然后，使用圆片的面积公式 S = 2πrL，就得到了圆锥的侧面积公式。在实际计算中，底径和侧长都可以通过算法或测量得到。这是一个简单但有效的方法。

圆锥侧长的求出与对圆锥侧面积计算的影响

在计算圆锥侧面积之前，我们首先需要求出圆锥的侧长。如果知道圆锥的侧长（l）和底径（r），则直接使用公式 S = πrl 就可以求出圆锥的侧面积。但是，如果只知道圆锥的底径和高度（h），则需要先求出侧长。在这种情况下，可以使用其中的方法求出侧长，l = √(r² + h²) ，求出侧长后，再使用公式 S = πrl 求出圆锥的侧面积。在实际应用中，应该精确测量圆锥的底径和高度，以保证计算的精确性。

圆锥侧面积计算的应用与实例分析

圆锥侧面积的计算广泛应用于各种工程和科学领域。例如，在建筑工程中，计算圆锥型截面的压力面积；在工业生产中，计算圆锥型切割面的压力面积；在医学中，定量圆锥的行为；在高等数学研究中，有关于缩线的长度的计算。在实际中，需要通过实验或者模拟等方法来确定其精确值。大多数实际问题需要考虑圆锥侧面的垂直面积，以保证计算的精确性。

圆锥侧面积计算中应注意的问题与复查方法

在计算圆锥侧面积的过程中，应该注意到一些问题。首先，要确保底径和侧长的测量精确性。如果测量不精确，则计算结果也会出现误差。第二，要选择适当的计算方法。如果使用错误的方法，则计算结果也会不精确。第三，要对计算结果进行复查。如果结果不合理，则需要寻找原因并进行改正。在实际计算中，应该准确判断圆锥的型形和精确的数据。