大于号小于号怎么区分？详解数学符号的应用与辨析

本文详细阐述了大于号小于号的区分方法，从基础概念到实际应用，深入浅出地讲解了这两个数学符号的用法，并结合不等式等数学知识进行了深入探讨。文章还涵盖了其在日常生活和数据分析中的应用，以及未来发展趋势，希望能帮助读者彻底掌握大于号小于号的区分方法，并提升数学应用能力。文章中还探讨了分数大小比较和不等式性质等长尾关键词。

认识大于号和小于号：基础概念及起源

大于号和小于号是数学中最重要的比较符号，分别表示“大于”和“小于”的关系。它们尖端指向较小的数，开口对着较大的数。这看似简单的设计，却蕴含着数学的精髓，精准地表达了数量间的差异。

追溯历史，大于号（>）和小于号（<）是由英国数学家托马斯·哈里奥特于17世纪初引入的。在此之前，人们常常使用文字来表达大小关系，例如“大于”、“小于”，这使得数学表达较为繁琐。哈里奥特的创新简化了数学语言，极大地提高了数学表达的效率和精确性。

我们可以从一些简单的例子来理解这两个符号：5 > 3 表示 5 大于 3；2 < 7 表示 2 小于 7。这些例子清晰地展示了大于号和小于号在数值比较中的应用，是理解这两个符号最基础的步骤。在学习过程中，反复练习和实践，才能真正熟练掌握这两种数学符号。

理解大于号和小于号的基础概念，对于后续学习不等式、方程等数学知识至关重要。许多复杂的数学问题，都离不开对数值大小关系的准确判断，而这正是大于号和小于号所提供的基本工具。

深入理解：不同数集中的应用及特殊情况

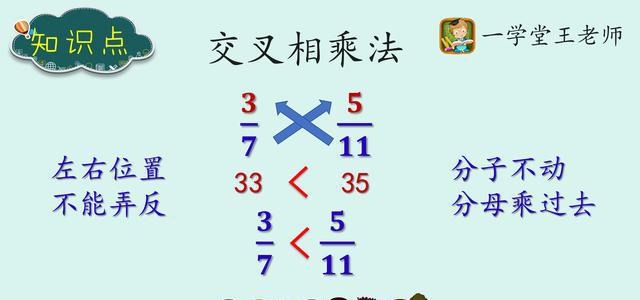
大于号和小于号的应用不仅限于整数，还扩展到分数、小数、实数等各种数集中。例如，在比较分数时，我们需要通分或转化为小数进行比较，从而判断哪个分数更大或更小。同样，在比较小数时，我们也需要关注小数点后的位数，才能准确判断大小关系。

值得注意的是，在某些特殊情况下，我们还需要考虑符号的优先级。例如，在含有括号的表达式中，我们需要先计算括号内的表达式，然后再进行大小比较。此外，在涉及到负数的比较时，也需要注意，例如 -5 < 2，虽然 -5 的绝对值大于 2，但 -5 仍然小于 2。这表明在进行大小比较时，不仅需要关注数值的绝对大小，还需要关注数的正负性。

此外，在计算机编程中，大于号和小于号也常常被用作逻辑运算符，用于判断两个数值或表达式的大小关系。例如，在if语句中，我们可以使用大于号或小于号来控制程序的执行流程，这在编写程序时非常重要。因此，理解大于号和小于号的精髓，不仅在数学领域至关重要，在计算机科学等其他领域也具有广泛的应用。

日常生活中的应用：从价格比较到数据分析

大于号和小于号并非只存在于数学课堂或教科书中，它们广泛应用于日常生活中的各个方面。例如，在购物时，我们经常会比较不同商品的价格，判断哪件商品更便宜。此时，大于号和小于号便能发挥其作用，帮助我们做出更明智的消费决策。

此外，在进行数据分析时，我们也经常会用到大于号和小于号来筛选数据。例如，我们可以根据某个指标的数值大小，筛选出符合特定条件的数据，从而更有效地进行数据分析。在数据分析中，数据的筛选和排序往往需要比较运算，大于号和小于号在这方面扮演着关键作用。

不仅如此，在很多图表中，我们也会看到大于号和小于号的使用。例如，在条形图中，我们可以用大于号和小于号来标注不同数据之间的比较关系。这使得图表更加直观易懂，方便人们快速地获取信息。

总而言之，大于号和小于号是日常生活和数据分析中不可或缺的工具。深入了解它们的使用方法，将提升我们分析问题和解决问题的能力。

不等式与大小比较：深入探索数学关系

大于号和小于号是构成不等式的基础元素。不等式是数学中用来表示两个表达式之间大小关系的式子，例如：x > 3，2y < 10 等。不等式在数学解题和证明中扮演着关键角色，掌握不等式性质是解题的关键。

不等式的基本性质包括：传递性（若a>b且b>c，则a>c）；加法性质（若a>b，则a+c>b+c）；乘法性质（若a>b且c>0，则ac>bc；若a>b且c<0，则ac

不等式的应用非常广泛，例如在经济学中，我们使用不等式来分析资源分配、价格波动等问题。在物理学中，不等式常被用来描述各种物理规律和现象，例如热力学第二定律。

学习不等式有助于培养我们的逻辑思维能力，提高我们分析和解决问题的能力。理解大于号和小于号在不等式中的作用，是掌握不等式技巧的重要环节。

总结与展望：数学符号的未来发展

大于号和小于号作为基础的数学符号，其简单而有效的表达方式，在数学发展史上具有里程碑式的意义，并持续在现代数学中发挥着不可替代的作用。 它们不仅是简单的比较符号，更是构建更复杂数学模型和进行数学推理的基石。

随着数学理论的不断发展和计算机技术的进步，对数学符号的表达和运算效率也提出了更高的要求。未来，可能会出现更多更精细的数学符号，以应对更加复杂的数学问题。 然而，大于号和小于号作为最基础和最直观的比较符号，其地位仍将稳固。

在数学教育领域，培养学生对大于号和小于号的理解和应用能力至关重要。 只有掌握了这些基础知识，学生才能更好地理解和掌握更高级的数学知识。 因此，加强对基础数学符号的教学，对于提高学生的数学素养和逻辑思维能力具有重要意义。