梯形的高怎么求公式？详解梯形面积计算及高求解方法

本文系统阐述了梯形的高怎么求公式，详细讲解了梯形面积计算及高求解方法，并结合等腰梯形、直角梯形等不同类型梯形，深入探讨了不同求解方法，并分析了在实际问题中的应用以及未来发展趋势，例如利用辅助线求解梯形的高、实际应用中梯形高求解等长尾关键词，希望能帮助读者全面掌握梯形高求解技巧。

梯形的高：公式推导与理解

梯形的高是指梯形两底之间垂直距离。求梯形的高，需要根据已知条件选择合适的公式。最基本的梯形面积公式为：S = (a+b)h/2，其中S表示梯形面积，a和b分别表示梯形的上下底长，h表示梯形的高。

如果已知梯形的面积S和上下底长a、b，则可以很容易地求出梯形的高h：h = 2S/(a+b)。这个公式是求梯形高最直接的方法，也是理解其他求高方法的基础。

例如，一个梯形面积为30平方厘米，上底为4厘米，下底为8厘米，则其高为：h = 2 * 30 / (4+8) = 5厘米。

理解这个公式的关键在于掌握梯形面积的计算原理，即把梯形转化为平行四边形和三角形的组合。

许多初学者在理解梯形高时容易混淆高和斜边。需要强调的是，梯形的高必须是垂直于两底的线段长度。

不同类型梯形的高的求解方法

根据梯形的不同类型，求高的方法也有所不同。

对于等腰梯形，我们可以利用等腰梯形的对称性，作高，将等腰梯形分割成两个直角三角形和一个矩形。通过勾股定理，结合已知条件（例如，上下底长和腰长），便可以求出梯形的高。

例如，一个等腰梯形，上下底分别为6cm和10cm，腰长为5cm，我们可以作高，得到一个直角三角形，其中一条直角边为(10-6)/2=2cm，斜边为5cm。根据勾股定理，高为√(5²-2²)=√21cm。

对于直角梯形，其中一个腰为高，直接利用已知条件即可求出梯形的高。

如果梯形是特殊的，例如是等腰梯形，已知腰长和底长，可以利用勾股定理求高。如果已知面积和上下底，则可以直接使用面积公式求高。需要根据已知条件灵活运用相关的几何知识。

利用辅助线求解梯形的高：几何方法的运用

• 作一条垂直于上下底的辅助线，将梯形分割成矩形和三角形。
• 利用勾股定理，根据已知条件求解三角形中的未知量。
• 根据已知的面积，运用梯形面积公式，反推求出梯形的高。
• 利用相似三角形性质，建立比例关系求解。
• 在实际应用中，灵活运用上述方法，选择最合适的解题思路。

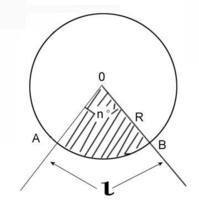
实际问题中的梯形高求解

在实际生活中，我们经常会遇到需要计算梯形高的问题。例如，在土木工程中，计算不规则地块的面积；在测量学中，测量山坡的坡度等等，都需要用到梯形的高。

解决这类问题，需要根据题目的具体描述，选择合适的公式和方法，并结合相关的几何知识。

例如，在测量一个梯形的山坡时，我们已知坡面距离，底边长度，且角度已知，可利用三角函数计算山坡的垂直高度即梯形的高。

在实际应用中，我们可能需要先将复杂图形分解成若干个梯形，然后分别计算每个梯形的高，再将结果进行累加。

解决实际问题的关键在于：仔细分析题目已知条件，选择合适的公式，将实际问题转化为数学模型。

梯形高求解公式的未来展望

随着科技的发展，计算机技术和人工智能技术的不断进步，梯形高求解方法将更加高效和便捷。

未来，基于图像识别的技术，可以快速、准确地识别和测量梯形的相关参数，自动计算梯形的高。这将极大简化计算过程，提高效率，并在更多领域得到广泛应用。

与此同时，更加智能化的计算工具和软件的开发，也将会为梯形高求解提供更大的便利。例如，通过输入梯形相关参数，软件可以自动计算并输出梯形的高，并提供详细的计算过程和结果解释，甚至可以处理更复杂的图形。

此外，未来研究的方向可能集中在如何更高效地求解一些复杂梯形的高，例如带有弧线的梯形、空间中的梯形等。