特征值怎么求？深入浅出矩阵特征值计算方法及应用场景

本文深入浅出地讲解了特征值怎么求，介绍了特征多项式法、幂法等多种计算方法，并分析了它们各自的优缺点及适用场景，最后探讨了特征值计算的应用前景及未来发展趋势，希望能够帮助读者更好地理解和掌握特征值计算的知识。文中提到的特征多项式法和幂法是求解特征值的两大核心方法，而特征值的应用则涵盖了物理、工程、图像处理等众多领域。

特征值与特征向量的基本概念

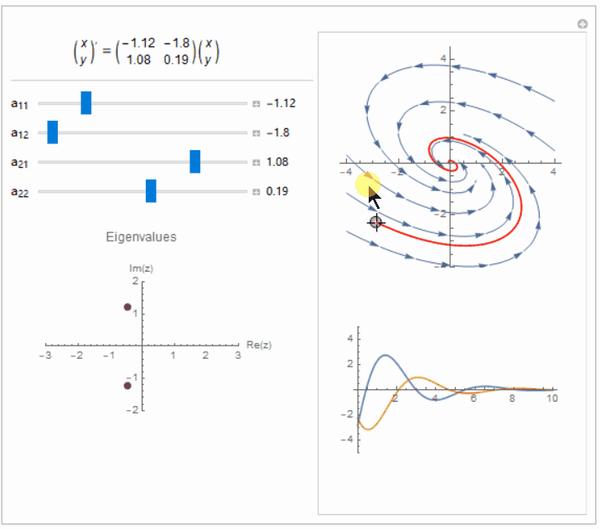
理解特征值怎么求，首先要明确特征值和特征向量的定义。对于一个 n 阶方阵 A，如果存在一个非零向量 x，使得 Ax = λx 成立，则称 λ 为矩阵 A 的特征值，x 为对应于特征值 λ 的特征向量。这里，λ是一个标量，表示向量x在矩阵A作用下的伸缩比例。

求解特征值的过程，实质上是寻找满足该方程式的 λ 和 x。这个方程可以转化为 (A - λI)x = 0，其中 I 是单位矩阵。由于 x 是非零向量，(A - λI) 必须是奇异矩阵，即它的行列式必须为零，也就是|A - λI| = 0。这个等式被称为特征方程，它的根就是矩阵 A 的特征值。

例如，一个简单的 2x2 矩阵，其特征值的求解过程可以直观地展现特征值计算的本质。通过计算特征多项式，我们可以找到特征值，然后代入方程求解特征向量。这个例子可以帮助初学者快速理解特征值的含义和计算步骤。

特征多项式法：求解特征值的核心方法

特征多项式法是求解特征值最常用的方法。其核心思想是根据特征方程 |A - λI| = 0，计算矩阵 A 的特征多项式。特征多项式是一个关于 λ 的多项式方程，其根就是矩阵 A 的特征值。

对于低阶矩阵，例如 2x2 或 3x3 矩阵，可以直接展开行列式计算特征多项式，然后求解多项式方程的根，从而得到特征值。

然而，对于高阶矩阵，直接计算行列式和求解多项式方程会变得非常复杂。这时，可以使用数值计算方法，例如 QR 算法或 Jacobi 方法，来近似求解特征值。这些数值方法在计算机科学和工程领域有着广泛的应用，尤其是在处理大型矩阵时具有显著的优势。数值方法的精度和效率是选择算法时需要重点考虑的因素，这直接关系到最终计算结果的准确性以及计算效率。

幂法及其改进：求解特征值的其他方法

除了特征多项式法，幂法也是一种常用的求解特征值的方法，尤其适用于求解绝对值最大的特征值。幂法的基本思想是通过迭代计算，不断将矩阵 A 作用于一个初始向量，最终使其收敛到与最大特征值对应的特征向量。

幂法简单易懂，计算量相对较小，但是收敛速度较慢，并且只能求解绝对值最大的特征值。为了克服幂法的不足，研究者们发展了一系列改进的幂法，例如反幂法、QR 算法等。这些改进后的算法可以提高计算效率，并可以求解其他特征值。例如，反幂法可以有效地求解最小特征值。

实际应用中，根据矩阵的特性和需要求解的特征值的性质，选择合适的算法至关重要。例如，对于大型稀疏矩阵，选择迭代法更有效率；而对于小型稠密矩阵，直接法可能更方便快捷。

特征值计算的应用场景及未来发展趋势

特征值计算在众多领域都有着广泛的应用，例如：在物理学中，用于分析振动系统、量子力学；在工程学中，用于分析结构稳定性、控制系统设计；在图像处理中，用于图像压缩、人脸识别。

随着大数据时代的到来和人工智能技术的飞速发展，对特征值计算的需求也日益增长。未来，高性能计算、并行算法以及更有效的数值方法的研究和发展将成为研究重点，以应对更大规模和更复杂矩阵的特征值计算挑战。

例如，量子计算技术的进步有望极大提高特征值计算的效率，从而推动人工智能、材料科学等领域的发展。同时，新的数值算法以及更强大的计算机硬件，会让特征值计算在更广泛的领域发挥更大的作用。