轻松掌握平方计算方法：从基本公式到高级应用技巧详解

本文详细阐述了平方怎么计算，从基本公式到实际应用，并介绍了快速计算技巧以及需要注意的误区。文章还探讨了不同类型数的平方计算方法，以及平方计算在生活中的广泛应用和未来发展趋势，例如面积计算、几何问题和数据统计等，旨在帮助读者全面掌握平方计算，提升数学能力。

平方计算的基本公式与方法

平方，简单来说，就是将一个数乘以自身。最基本的平方计算公式就是：a² = a × a，其中a代表任何一个数字。例如，5的平方（5²）就是5 × 5 = 25；12的平方（12²）就是12 × 12 = 144。

理解了这个基本公式后，我们就可以进行各种数字的平方计算。对于整数的平方计算相对简单，可以直接进行乘法运算。但是，对于小数或分数的平方计算，则需要一些技巧。例如，计算0.5的平方，我们可以先将0.5写成分数形式1/2，然后计算(1/2)² = 1/4 = 0.25。又例如，计算(2/3)²，则可以计算成(2/3)×(2/3) = 4/9。

除了直接运用公式进行计算外，我们还可以利用一些辅助工具，比如计算器，快速得到结果。现在许多手机和电脑都自带计算器功能，方便快捷。当然，熟练掌握乘法口诀表也能提高平方计算的速度和准确性。

不同数的平方计算方法：整数、分数、小数及负数

掌握平方计算的关键在于理解其基本原理，并根据不同类型的数灵活运用计算方法。

对于整数，可以直接进行乘法运算。例如，计算 8 的平方，我们只需计算 8 × 8 = 64。

对于分数，我们需要先将分子和分母分别平方，然后再化简。例如，计算 (3/4)²，我们先计算 3² = 9 和 4² = 16，然后得到 (3/4)² = 9/16。

对于小数，我们可以将其转换为分数进行计算，或者直接使用计算器计算。例如，计算 0.25 的平方，我们可以将其转换为分数 1/4，然后计算 (1/4)² = 1/16 = 0.0625，也可以直接使用计算器计算。

对于负数，其平方结果为正数。这是因为负数乘以负数等于正数。例如，(-5)² = (-5) × (-5) = 25。

平方计算在实际生活中的应用及案例分析

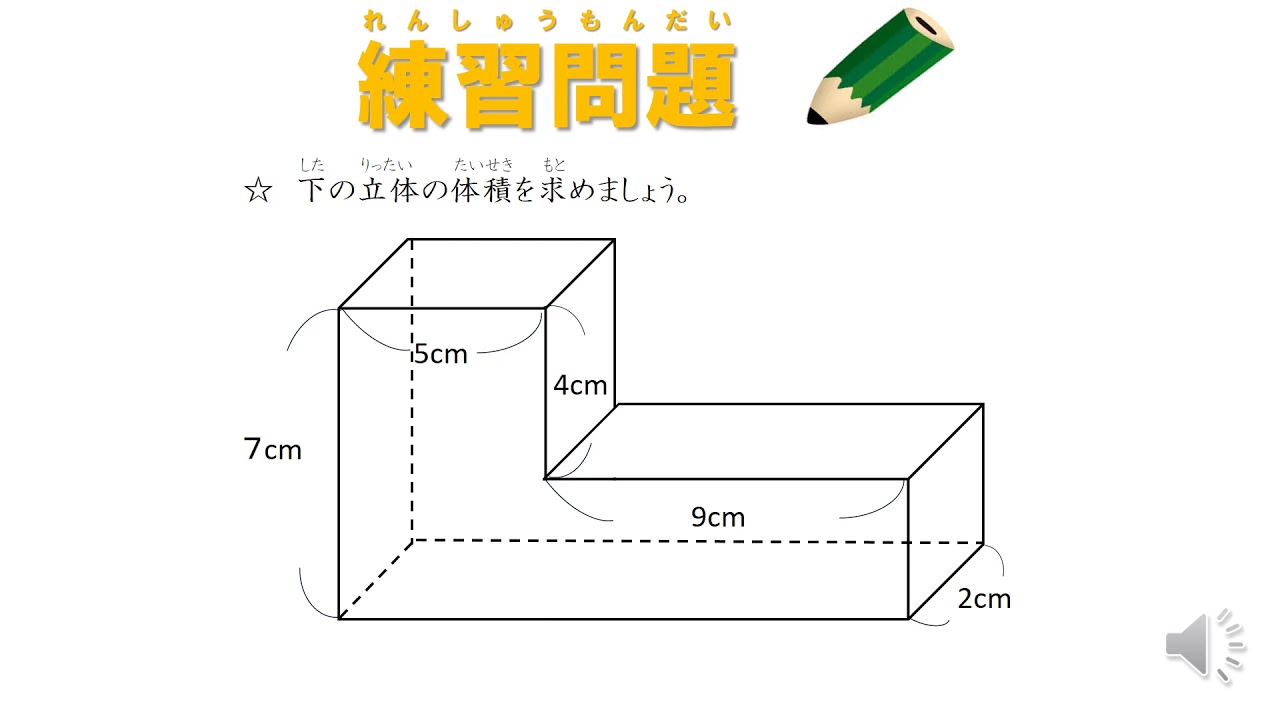
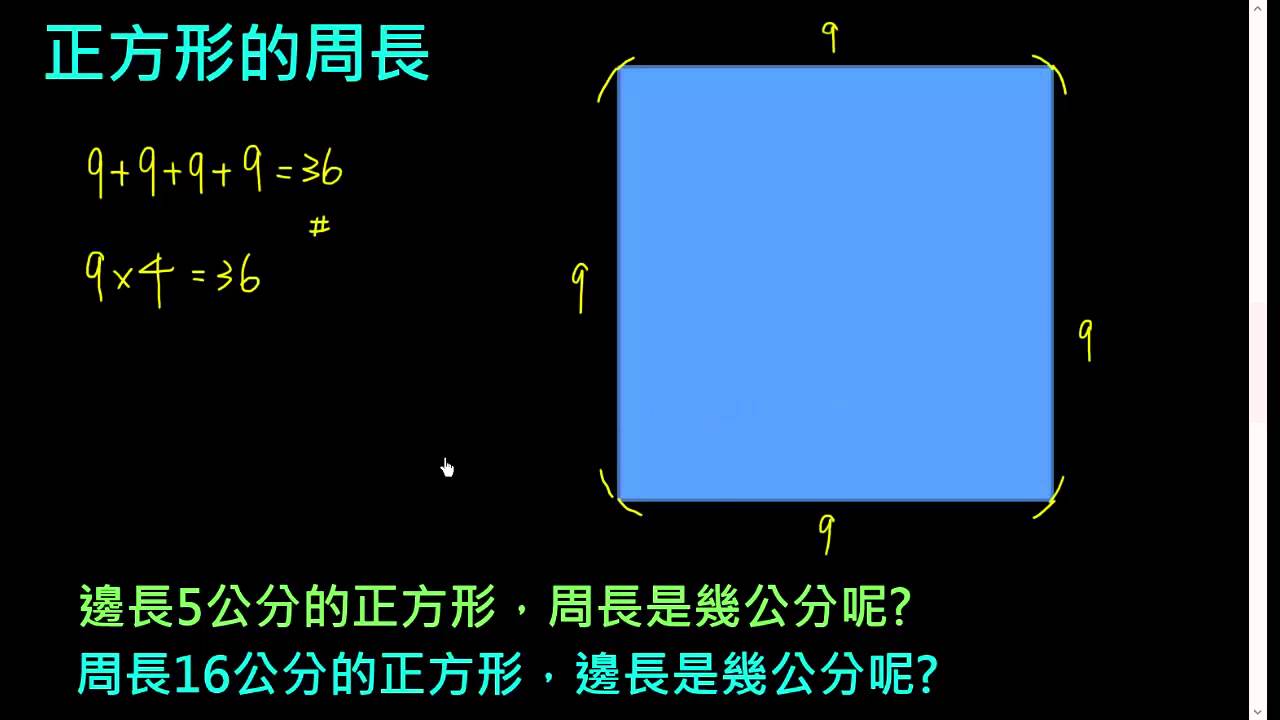
• 面积计算：正方形、长方形等图形的面积计算都与平方密切相关，例如计算边长为 5 米的正方形面积，直接计算 5²=25 平方米。
• 几何问题：在几何问题中，例如计算圆的面积，需要用到半径的平方。
• 物理学：在一些物理公式中也经常用到平方，例如计算速度、加速度等。
• 工程计算：许多工程项目的设计和施工都涉及到平方的计算，例如建筑面积计算、管道尺寸计算。
• 数据统计：在数据分析中，平方经常用于计算方差、标准差等统计指标，用于评估数据的离散程度。

快速平方计算技巧及误区分析

除了基本公式外，还有一些技巧可以帮助我们更快地进行平方计算。例如，对于一些特殊的数字，我们可以运用一些简单的公式进行快速计算。例如，(a+1)² = a²+2a+1，我们可以利用已知数的平方快速计算相邻数的平方。一些常用的平方数，我们可以记忆下来，方便计算。此外，还可以通过拆分数字等方法进行简便计算，例如，15²=(10+5)² = 100+100+25=225。

然而，在进行平方计算时也有一些误区需要注意。例如，许多人会误以为(a+b)²=a²+b²，这是错误的。正确的公式应该是(a+b)² = a²+2ab+b²。又如，计算带有小数的平方时，容易出现计算错误，这时使用计算器是比较好的方法。

平方计算的未来发展趋势与展望

随着科技的发展，计算工具的不断进步，平方计算的方式将会更加多样化和便捷化。例如，人工智能的应用将使得平方计算更加自动化和智能化，减少人工计算的错误率，提高效率。未来的计算工具可能能够实时进行复杂的平方计算，并提供多种计算结果和分析。同时，平方计算的应用场景也会更加广泛，例如，在虚拟现实、人工智能等领域，平方计算将会发挥更大的作用。

当然，随着计算工具的不断发展，我们更应该关注的是计算思维的培养。培养良好的计算习惯，提升逻辑思维能力，才能够更好地利用计算工具，更好地解决实际问题。