轻松掌握公倍数求法：技巧、方法及应用场景详解

本文详细讲解了公倍数的求法，包括最小公倍数和最大公倍数的计算方法，并结合实际案例分析了不同方法的优缺点，例如短除法和分解质因数法，以及最大公约数与最小公倍数的关系。文章还探讨了公倍数在实际生活中的应用，例如时间安排和资源分配。最后，对公倍数求解方法进行了总结和展望，强调了扎实的数学基础在解决实际问题中的重要性。

理解公倍数的概念及求法基础

求公倍数是数学学习中的重要环节，理解其概念是掌握计算方法的关键。公倍数是指几个整数共有的倍数。例如，6 和 8 的倍数分别有：6：6，12，18，24，30，36…；8：8，16，24，32，40，48…；它们共有的倍数就是它们的公倍数，如 24，48 等。

求公倍数最基本的方法是列举法：分别列出每个数的倍数，然后找出这些倍数中相同的数，这些相同的数就是它们的公倍数。例如，求 4 和 6 的公倍数，列出 4 的倍数：4, 8, 12, 16, 20, 24, 28…；列出 6 的倍数：6, 12, 18, 24, 30, 36…；可以看出，12 和 24 都是它们的公倍数。这种方法简单易懂，但对于较大的数或多个数来说，效率较低，容易遗漏。

理解公倍数的概念，是学习最小公倍数和最大公倍数的基础，也是后续学习分数、比和比例等数学概念的重要前提。很多学生在小学阶段就接触到公倍数的概念，但对于如何高效准确地求解公倍数却存在困惑。因此，掌握多种求解方法和技巧，对提高数学学习效率至关重要。

最小公倍数的求法：短除法与分解质因数法

在众多公倍数中，最小公倍数 (LCM) 具有特殊的意义。它在分数运算、解决实际问题等方面都有广泛的应用。求最小公倍数，常用的方法有短除法和分解质因数法。

短除法是一种简洁高效的方法。以求 12、18 和 24 的最小公倍数为例，将这三个数用短除法进行分解：

2 | 12 18 24

3 | 6 9 12

2 | 2 3 4

| 1 3 2

将所有除数相乘：2 × 3 × 2 × 2 × 3 = 72，所以 12、18 和 24 的最小公倍数是 72。

分解质因数法也是一种常用的方法。先将每个数分解成质因数的乘积，然后找出所有质因数中指数最大的那些，将它们相乘即得到最小公倍数。例如，12 = 2² × 3，18 = 2 × 3²，24 = 2³ × 3。则最小公倍数为 2³ × 3² = 72。

这两种方法各有优缺点，短除法更加直观，分解质因数法则更能体现数的本质特征，选择哪种方法取决于具体的数字和个人习惯。

最大公约数与最小公倍数的关系：互质数的特殊情况

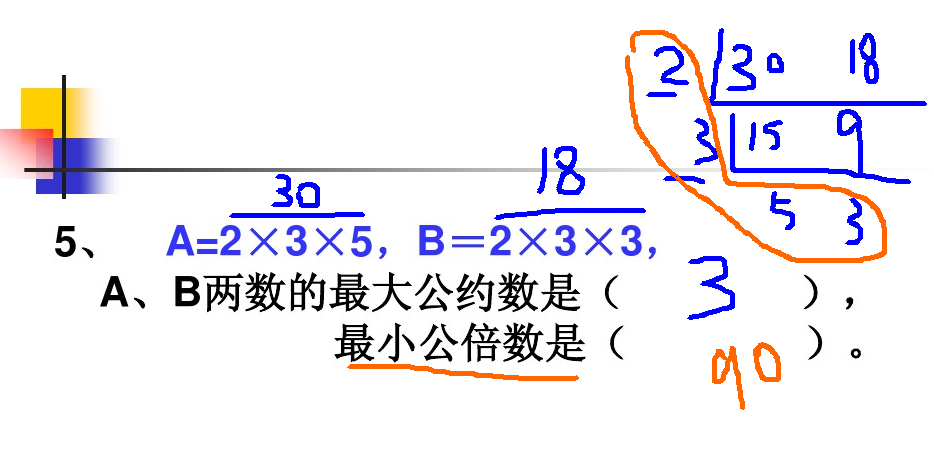
最大公约数 (GCD) 与最小公倍数 (LCM) 密切相关。对于两个数 a 和 b，它们的最小公倍数和最大公约数存在一个重要的关系：a × b = GCD(a, b) × LCM(a, b)。

利用这个关系，我们可以通过求最大公约数来间接求最小公倍数。例如，要计算 12 和 18 的最小公倍数，首先求它们的最大公约数：12 = 2² × 3，18 = 2 × 3²，最大公约数是 6。那么，最小公倍数为 (12 × 18) ÷ 6 = 36。

当两个数互质时，即它们的最大公约数为 1，那么它们的最小公倍数就是这两个数的乘积。例如，5 和 7 互质，它们的最小公倍数是 5 × 7 = 35。这个特性在求解最小公倍数时可以简化计算过程，提高效率。

理解最大公约数与最小公倍数的关系，可以帮助我们更好地理解数的性质，并找到更简便的计算方法，从而在解决数学问题时更加灵活和高效。

公倍数在实际生活中的应用

公倍数的概念并非只存在于数学课本中，它在实际生活中也有着广泛的应用。例如，在安排工作计划时，需要考虑不同任务的周期。假设一个任务每 3 天完成一次，另一个任务每 5 天完成一次，那么这两个任务同时完成的周期就是它们的最小公倍数，即 15 天。

在一些机械设备的维修保养中，也常涉及到公倍数的计算。例如，某个机器的部件 A 需要每 6 个月更换一次，部件 B 需要每 8 个月更换一次，为了确保两个部件的更换时间能重合，就需要计算 6 和 8 的最小公倍数，即 24 个月，此时这两个部件需要一起更换。

此外，在一些涉及到时间安排、资源分配等实际问题中，公倍数的概念也扮演着重要的角色。例如，公共汽车的班次设计，不同列车的发车时间等，都可能用到公倍数的原理。合理地应用公倍数原理，能够帮助我们优化资源分配、提高效率，并避免不必要的浪费。

公倍数求解方法的总结与展望

本文总结了多种求解公倍数的方法，包括列举法、短除法、分解质因数法以及利用最大公约数求最小公倍数的方法。每种方法都有其优缺点，选择哪种方法取决于具体的问题和个人习惯。对于简单的数字，列举法或许足够；对于较大的数字或多个数字，短除法或分解质因数法更为高效。而利用最大公约数和最小公倍数的关系，则可以进一步简化计算。

在未来，随着计算机技术的发展，我们可以期待更多更便捷的算法和工具来辅助公倍数的求解。例如，一些数学软件或计算器可以快速计算出任意多个数的最小公倍数和最大公约数。这将进一步提高我们解决相关问题的效率。但无论技术如何发展，扎实的数学基础仍然是解决实际问题的关键。理解公倍数的概念和掌握各种计算方法，将使我们能够更好地应对各种实际问题，并从更深入的角度理解数学的魅力。