法向量怎么求？详解法向量计算方法及应用场景

本文系统地阐述了法向量怎么求，涵盖了平面法向量和曲面法向量的计算方法，并分析了法向量在计算机图形学等领域的应用及误差问题。文章指出，准确计算法向量对于诸多领域至关重要，未来法向量计算方法的改进和应用将更加广泛。

平面法向量的求解方法

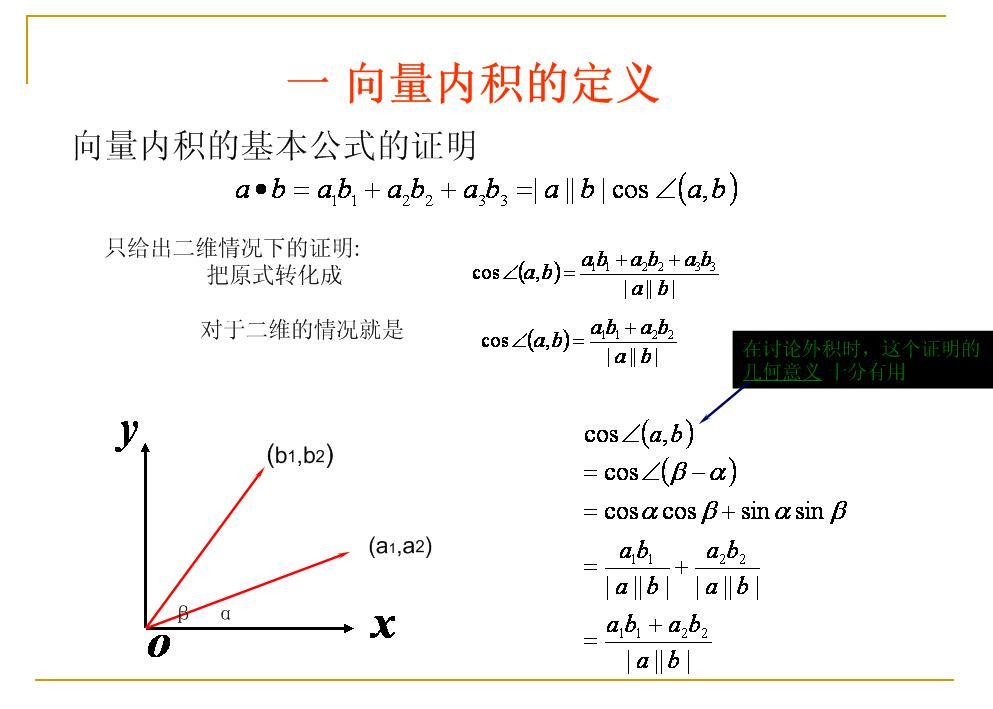
求解平面法向量是向量计算中的一个基础问题，其方法多种多样，取决于已知条件的不同。

如果已知平面上三个不共线的点 A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3)，我们可以先求出向量 AB = (x2-x1, y2-y1, z2-z1) 和向量 AC = (x3-x1, y3-y1, z3-z1)。平面法向量 n 为 AB 和 AC 的向量积，即 n = AB × AC。向量积的计算方法是：

nx = (y2-y1)(z3-z1) - (z2-z1)(y3-y1)

ny = (z2-z1)(x3-x1) - (x2-x1)(z3-z1)

nz = (x2-x1)(y3-y1) - (y2-y1)(x3-x1)

最终得到平面法向量 n = (nx, ny, nz)。

另一种情况是，已知平面的方程 Ax + By + Cz + D = 0，则平面法向量 n = (A, B, C)。这是因为平面方程的系数正好是其法向量的坐标。

例如，对于平面 2x + 3y - z + 5 = 0，其法向量为 n = (2, 3, -1)。

选择哪种方法取决于已知条件，需要根据实际情况灵活选择。

曲面法向量的求解

曲面法向量的求解相对复杂，通常需要用到偏导数的概念。对于一个隐式方程表示的曲面 F(x, y, z) = 0，其法向量 n 在点 (x0, y0, z0) 处的表达式为：

n = (∂F/∂x, ∂F/∂y, ∂F/∂z)|_(x0, y0, z0)

其中，∂F/∂x, ∂F/∂y, ∂F/∂z 分别表示 F 对 x, y, z 的偏导数。在具体计算时，需要先求出偏导数，然后代入点 (x0, y0, z0) 的坐标进行计算。

对于参数方程表示的曲面，情况则更为复杂。如果曲面由参数方程 r(u, v) = (x(u, v), y(u, v), z(u, v)) 给出，则其法向量可以由两个偏导向量 r_u 和 r_v 的向量积求得：

n = r_u × r_v

其中，r_u = (∂x/∂u, ∂y/∂u, ∂z/∂u) 和 r_v = (∂x/∂v, ∂y/∂v, ∂z/∂v) 分别是 r 对 u 和 v 的偏导向量。

求解曲面法向量需要扎实的微积分基础。一些复杂的曲面可能需要采用数值计算的方法来逼近法向量。

法向量在计算机图形学中的应用

在计算机图形学中，法向量是至关重要的概念。它决定了表面的方向，用于计算光照效果、碰撞检测等。

例如，在光照计算中，法向量用于计算光线与表面的入射角，从而确定表面的明暗程度。Phong光照模型就广泛使用了法向量。

此外，在碰撞检测中，法向量可以帮助判断两个物体是否发生碰撞，以及碰撞发生的位置和方向。

在三维建模软件中，法向量也用于控制模型的表面细节。一个正确的法向量可以使得模型表面更加平滑，反之则可能出现明显的瑕疵。

总而言之，法向量在计算机图形学中扮演着非常重要的角色，其计算方法和准确性直接影响到最终渲染效果的质量。

法向量求解的误差分析及改进方法

在法向量的实际计算中，由于数值计算的精度限制以及模型自身的误差，可能会导致计算结果出现一定的偏差。

例如，在使用浮点数进行计算时，舍入误差会累积，影响法向量的准确性。对于复杂曲面，采用数值方法计算法向量时，网格密度也会影响精度。

为了减小误差，可以采用一些改进方法。例如，可以使用更高精度的浮点数类型进行计算；对于曲面法向量，可以通过增加网格密度来提高精度；也可以使用一些数值算法来提高计算的稳定性。

此外，还需要注意对计算结果进行归一化处理，以确保法向量的长度为1，从而保证计算结果的正确性。在实际应用中，通常需要根据具体情况选择合适的误差控制策略，以平衡计算精度和效率。

法向量在其他领域的应用及未来展望

• 物理学中的应用：法向量在描述力、电场等物理量时经常用到，例如计算压力、张力等。
• 工程学中的应用：法向量在结构力学、流体力学等领域都有重要的应用。例如，计算物体受力方向和大小。
• 医学成像中的应用：法向量在医学图像处理中被用于描述器官和组织的形状和表面特性。
• 人工智能领域的应用：法向量在计算机视觉和机器学习中也有广泛的应用，例如，三维模型重建。
• 游戏开发中的应用：游戏开发中，法向量用于计算光照、阴影、以及碰撞检测等，保证游戏的真实性和流畅性。