中心对称图形怎么判断？解析中心对称图形判定方法及应用

本文深入浅出地讲解了中心对称图形怎么判断，详细阐述了中心对称图形的概念、判定方法及应用，并对学习中常见的误区进行了分析，旨在帮助读者快速掌握中心对称图形的判断技巧。文章结合实例分析，深入探讨了中心对称图形的判定方法，包括折叠法和旋转法，并介绍了中心对称图形在日常生活中的应用。通过学习本文，读者可以更好地理解中心对称图形，提高几何学习效率。

中心对称图形的概念及基本特征

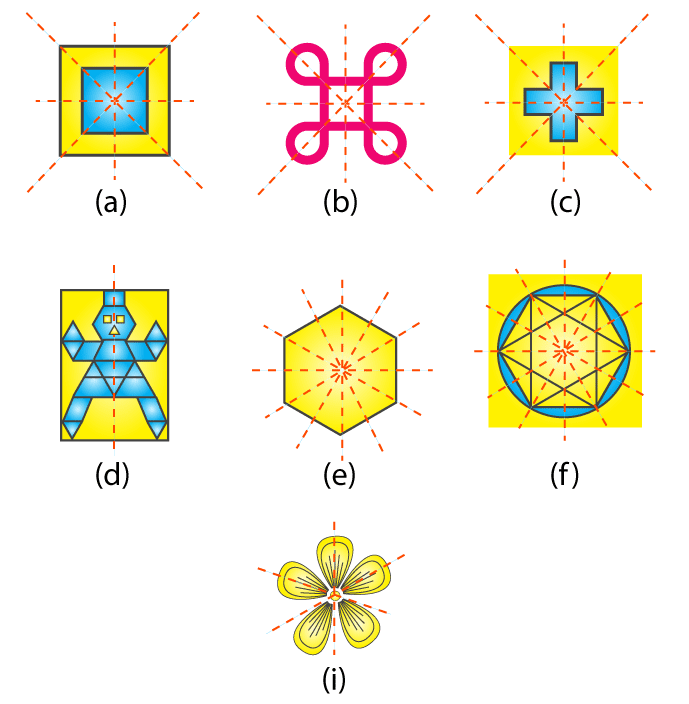
中心对称图形，简单来说，就是图形上任意一点与对称中心连线的另一端，也存在于图形上。判断一个图形是否为中心对称图形，关键在于寻找对称中心。对称中心是图形旋转180°后能与自身重合的关键点。

例如，正方形、矩形、圆形等都是典型的中心对称图形。正方形的对称中心在其两条对角线的交点；矩形也是如此；而圆形的对称中心便是其圆心。

需要注意的是，中心对称图形必须满足旋转180°后与自身重合的条件，不能有任何部分出现偏差。这要求图形具有高度的对称性，在寻找对称中心时，需要仔细观察图形的各个组成部分。

一些看似简单的图形，例如某些不规则的星形，需要仔细观察其旋转180°后的情况，才能准确判断是否具有中心对称性。这需要一定的空间想象力和几何分析能力。

中心对称图形的判定方法：折叠法与旋转法

判断中心对称图形，常用的方法主要有两种：折叠法和旋转法。

折叠法：假设存在对称中心，将图形沿过对称中心的任意直线折叠，观察折叠后的两部分图形是否完全重合。如果无论怎么折叠，两部分图形都完全重合，则该图形为中心对称图形。此方法直观易懂，适合简单图形的判断。例如，我们可以用一张纸剪出一个正方形，然后尝试沿不同的直线折叠，观察是否能完全重合。

旋转法：将图形旋转180°，观察旋转后的图形是否与原图形完全重合。如果完全重合，则该图形是中心对称图形。旋转法比折叠法更具普遍性，能判断更为复杂的图形。例如，判断一个不规则星形是否为中心对称图形，折叠法可能会比较困难，而旋转法则能更清晰地展现其对称性。

两种方法各有优劣，实际应用中可以结合使用，提高判断的准确性。

中心对称图形的常见误区及注意点

• 误认为所有对称图形都是中心对称图形。例如轴对称图形并非都是中心对称图形，线段、等腰三角形等都是轴对称图形，但它们并非中心对称图形。
• 忽略图形细节，导致判断失误。在判断复杂图形时，需要仔细观察图形的每一个部分，确保旋转180度后能完全重合。
• 仅凭直觉判断，缺乏严谨的逻辑推理。判断中心对称图形需要运用几何知识和逻辑推理，不能仅凭直觉判断。
• 对称中心不唯一。一个中心对称图形只有一个对称中心，多个对称中心的图形不是中心对称图形。
• 无法准确找到对称中心。在寻找对称中心时，可以尝试画出图形的对角线或寻找图形的中心点。

中心对称图形在日常生活中的应用

中心对称图形广泛存在于我们的生活中，许多艺术品、建筑物、标志等都应用了中心对称的原理，体现了对称的美感和平衡感。

例如，许多国家的国旗都采用了中心对称的设计，例如瑞士国旗就是一个典型的中心对称图形。许多建筑物的设计也体现了中心对称的理念，例如故宫太和殿，其建筑布局就具有明显的中心对称特征。

此外，在日常生活用品中，也经常可以看到中心对称图形的身影，例如一些餐具、装饰品等，这些物品的设计中都体现了中心对称的美感和实用性。

中心对称图形不仅具有美学价值，还在工程设计、科学研究等领域有着广泛的应用，例如在机械设计中，许多零件的设计都遵循中心对称的原理，以保证其平衡性和稳定性。

中心对称图形的学习方法与技巧

学习中心对称图形，需要结合理论知识和实践操作。首先，要理解中心对称图形的定义和基本特征，掌握判断中心对称图形的两种主要方法——折叠法和旋转法。

其次，要多做练习，通过大量的练习来提高自己判断中心对称图形的能力。在做题过程中，要认真分析题目，找出图形的对称中心，并通过折叠或旋转的方法来判断图形是否为中心对称图形。

此外，还要注意一些常见的误区和注意点，避免由于粗心大意而导致判断失误。

最后，建议大家可以尝试使用一些几何绘图软件，例如GeoGebra等，来辅助自己学习中心对称图形。通过软件的辅助，可以更好地理解中心对称图形的特性，提高学习效率。