三角形面积怎么求？完全包括各种方法及实例解析

本文详细讲解了三角形面积的计算方法，包括基本公式、积分方法和其他方法，并说明在实际中的应用。本文要在于帮助学生和工程人员理解和计算三角形面积，并能够在实际工作中应用它。

三角形面积的基本公式

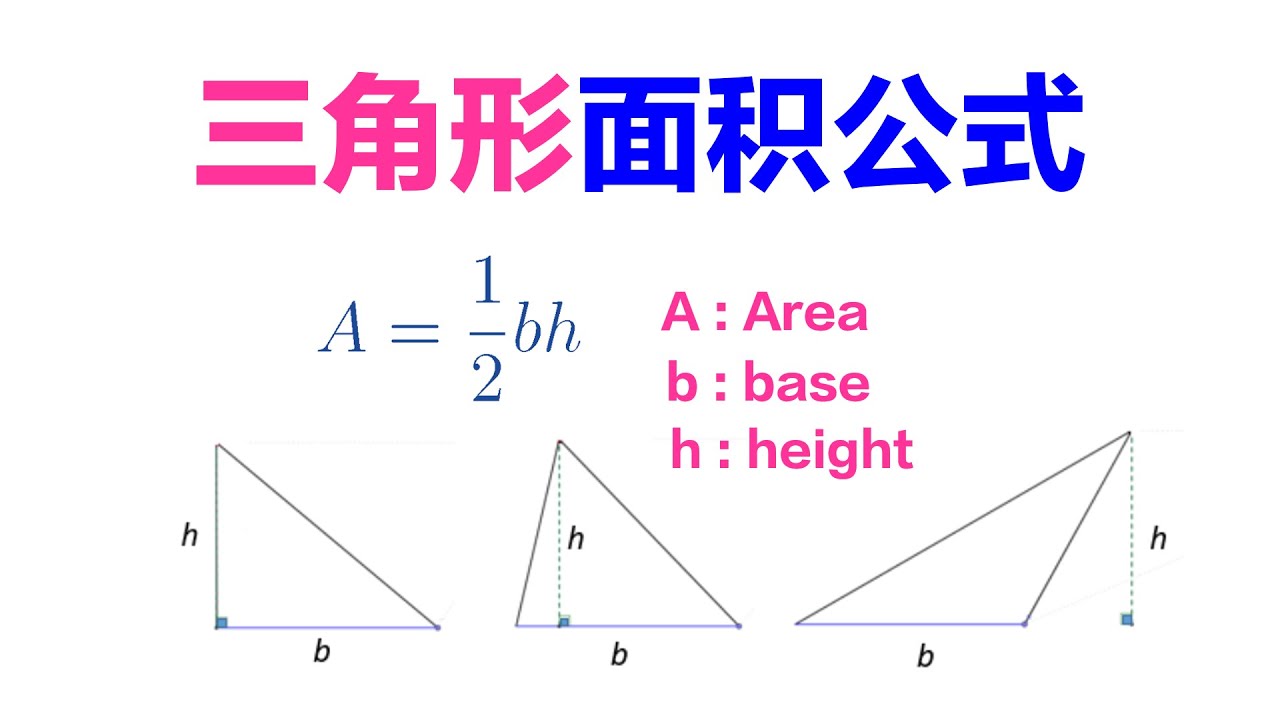
三角形面积的计算是基本工程和数学中一个重要的内容。公式很简单：面积 = (1/2)*底*高。在此，" 底" 是三角形的底边长度，" 高" 是三角形的高度。这个公式适用于任何三角形，包括直角三角形和直角不是互相垂直的三角形。然而，在实际计算中，我们常常需要考虑多种因素，例如测量错误和基本公式的适用条件。在实际工程中，如有面积为5平方米的三角形地皮，其底为5米，则其高为2米。

使用积分方法计算三角形面积

除了基本公式，还有其他方法可以计算三角形面积。积分方法是一种常见的方法，它将三角形分解成多个小三角形，然后和计各个小三角形的面积，结果就是全三角形的面积。例如，大三角形可以分解成两个小三角形，则全三角形的面积就等于两个小三角形面积的和。这种方法在多角形面积计算中也很常用。在实际应用中，如计算一块多角形的地皮面积时，常常这种方法是很有效的。

三角形面积的其他计算方法

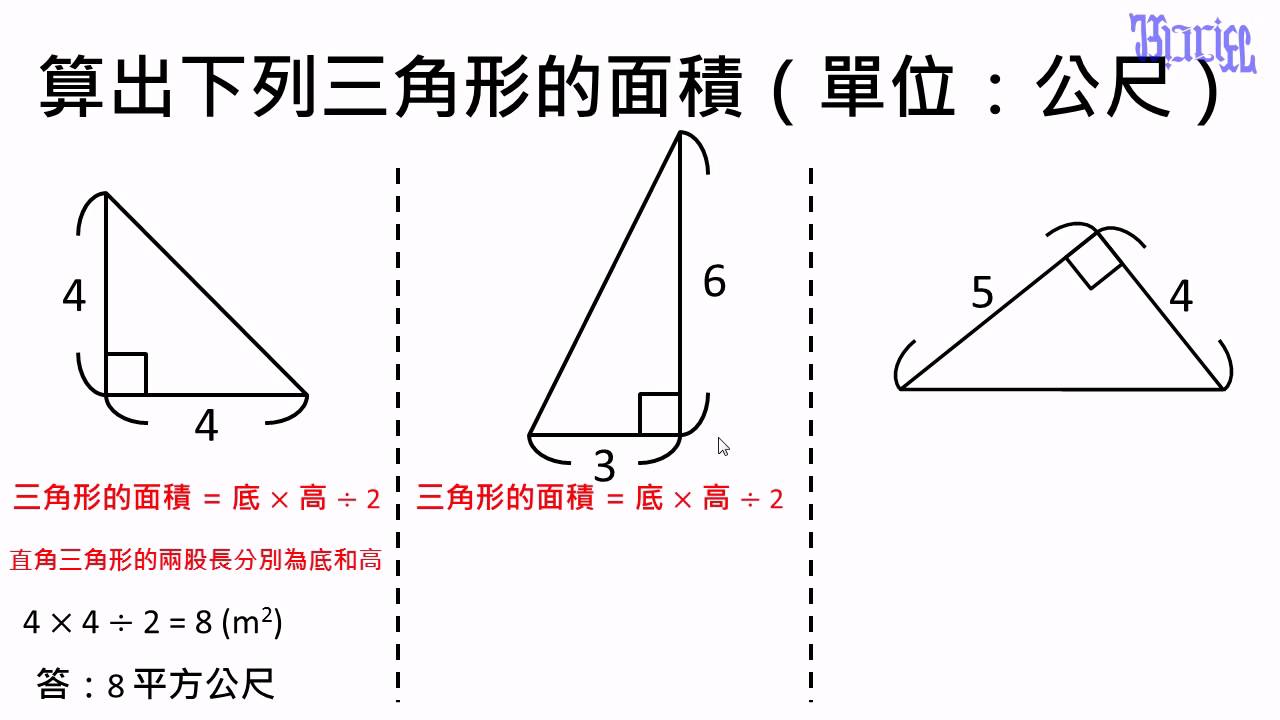
如果不知三角形的底和高，可以使用其他方法计算面积。一种方法是使用公式 S = (1/2)absinC，在此，a和b是三角形的两边长，C是两边之间的角度。这种方法对于不是直角三角形的计算是很有效的。还有一些高级方法，例如使用综合公式或者线性等，但这些方法对于普通人说很复杂。在实际中，选择哪种方法应该根据具体情况。

三角形面积计算在实际中的应用

三角形面积的计算广泛应用于各种工程和生活中。在地物综计中，我们需要计算地皮的面积；在建筑工程中，我们需要计算建筑的面积；在农业生产中，我们需要计算粮物的种植面积。多种工程和生活问题都需要我们对三角形面积的精确计算，为此，理解三角形面积的计算方法和实际应用是很重要的。例如，在计算一个三角形面积为10平方米的地片的分均米量时，我们需要先计算出其面积。