标准正态分布表怎么看？详解标准正态分布表的查找方法及应用技巧

本文深入浅出地讲解了标准正态分布表怎么看，包括其基础概念、查找方法、实际应用以及局限性等方面。通过学习本文，读者可以掌握标准正态分布表的应用技巧，并能更好地理解和应用正态分布在实际问题中的分析，例如如何使用标准正态分布表查询方法来计算正态分布概率，以及标准正态分布表在实际应用中的优势与局限性。

理解标准正态分布表：基础概念与结构

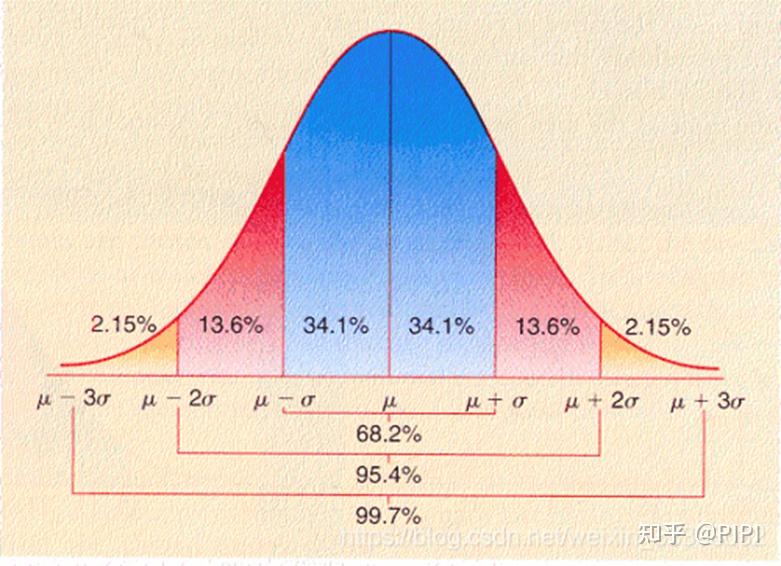
标准正态分布表，也称为Z表，是统计学中不可或缺的工具，它记录了标准正态分布曲线下不同Z值对应的概率值。理解标准正态分布表，首先要了解标准正态分布的概念：它是一种特殊的正态分布，其均值为0，标准差为1。这意味着，任何正态分布都可以通过标准化转化为标准正态分布，方便我们进行比较和分析。

标准正态分布表通常是一个表格，横轴代表Z值的整数部分和小数点后第一位，纵轴代表Z值的小数点后第二位，表内数值代表Z值左侧的概率。例如，查找Z=1.96的概率，找到横轴1.9，纵轴0.06，对应的表内数值即为0.9750，表示Z值小于1.96的概率为97.5%。

掌握这个基本原理，我们就能开始使用标准正态分布表进行计算。需要注意的是，不同的标准正态分布表可能略有差异，有些表格只给出了正值部分的概率，负值部分的概率可以通过对称性来计算。例如，Z=-1.96的概率等于1-0.9750=0.0250。

标准正态分布表的查找方法：步骤与技巧

查找标准正态分布表并非难事，只要掌握了正确的步骤和技巧，就能快速准确地找到所需概率值。首先，确定你需要查找的Z值，将Z值分解为整数部分和小数点后第一位以及小数点后第二位。例如，Z值为1.23，则整数部分和小数点后第一位为1.2，小数点后第二位为0.03。

然后，在标准正态分布表中找到对应的行和列。行对应整数部分和小数点后第一位，列对应小数点后第二位。找到行和列的交汇点，表内的数值就是Z值左侧的概率。

查找过程中需要注意一些细节：

* 表格通常只提供正Z值的概率，负Z值的概率可以通过公式计算：P(Z < -z) = 1 - P(Z < z)

* 对于Z值的小数点后第三位及以后的数值，可以进行四舍五入处理，或者通过线性插值法提高精度，但对于一般应用来说，四舍五入即可。

* 可以多次查表，然后相加或相减，根据实际问题来计算最终的概率。

例如，如果想知道Z值在1.5到2.0之间的概率，则需查找Z=2.0的概率和Z=1.5的概率，然后相减即可。

标准正态分布表的实际应用：案例分析与拓展

• 在质量控制中，可以使用标准正态分布表评估产品的合格率。
• 在金融领域，标准正态分布表可以用于风险评估和投资组合优化。
• 在医学研究中，可以使用标准正态分布表分析临床试验数据，检验药物疗效。
• 在心理学研究中，标准正态分布表可以用于分析心理测试结果，评估被试者的认知能力。
• 在社会学研究中，标准正态分布表可以用于分析社会调查数据，了解社会现象的分布规律。

标准正态分布表的局限性与未来发展趋势

标准正态分布表虽然应用广泛，但也存在一些局限性。首先，标准正态分布表只适用于标准正态分布，对于非标准正态分布，需要先进行标准化变换。其次，标准正态分布表只能提供近似值，精度有限，对于一些高精度的计算，可能需要采用更精确的数值方法。

此外，随着计算机技术的发展，越来越多的统计软件可以进行更精确的正态分布概率计算，无需依赖查表。但理解标准正态分布表的基本原理仍然具有重要意义，这有助于加深对正态分布的理解，也为理解更复杂的统计方法奠定基础。

未来，标准正态分布表可能会逐渐被更先进的计算工具所取代，但其作为统计学入门教学的工具，仍将发挥作用。理解它的原理，依然有助于理解统计学的核心概念。

总结：熟练掌握标准正态分布表的应用

总而言之，标准正态分布表是统计学中一个重要的工具，掌握其使用方法对于理解和应用正态分布至关重要。通过理解其基本原理、查找方法以及实际应用，我们可以更好地利用这个工具解决实际问题。尽管未来可能会有更先进的工具出现，但理解标准正态分布表的原理依然有助于我们更好地理解统计学，并为学习更高级的统计方法打下坚实的基础。熟练掌握标准正态分布表的应用，对于从事数据分析、统计研究等工作的人员而言，具有重要的实用价值。