本文深入探讨了年平均增长率的计算方法,从公式推导、不同数据类型的处理,到实际应用及局限性分析,并提出了更准确计算和解读的建议。文章通过案例分析,阐明了年平均增长率在经济学、财务管理和市场营销等领域的应用,以及如何避免其局限性带来的误解,最终帮助读者全面掌握年平均增长率的计算和应用,特别是关于如何计算不同类型数据的年平均增长率,以及解读结果的技巧。
年平均增长率计算公式及步骤详解
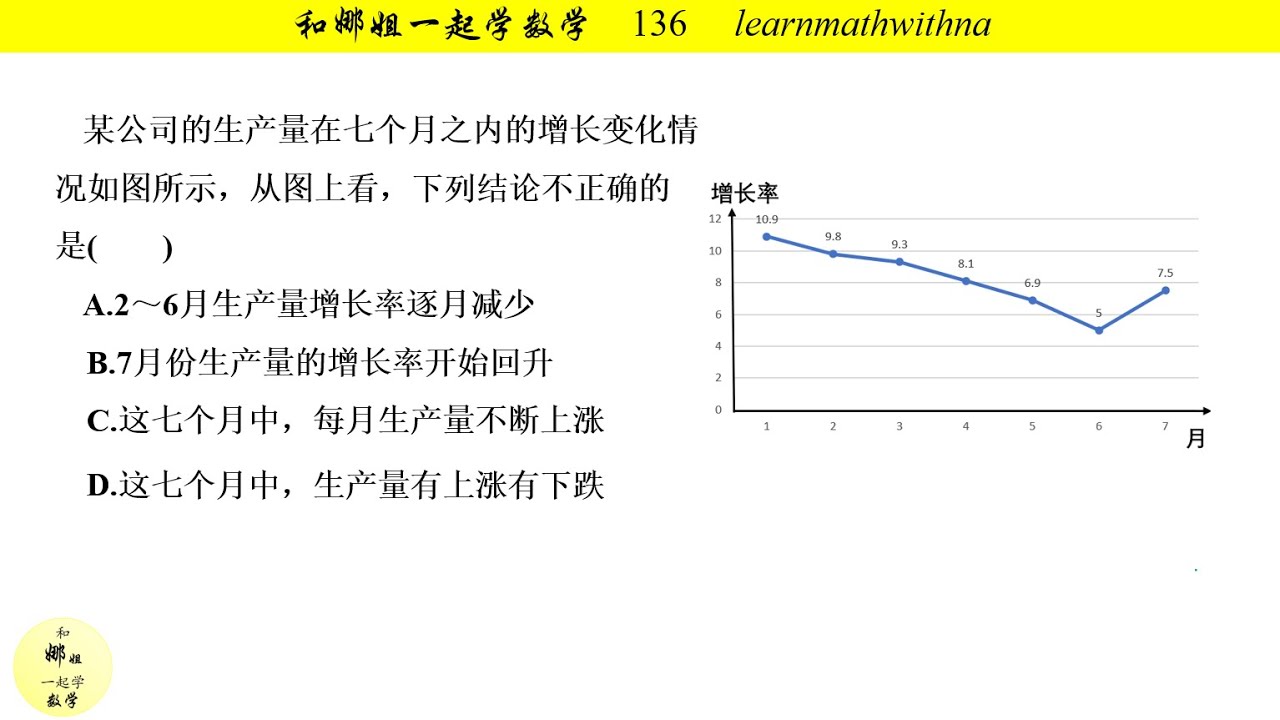
年平均增长率,指的是某指标在一段时间内的平均增长速度。准确计算年平均增长率对于评估经济增长、企业业绩或投资回报至关重要。
最常用的计算方法是几何平均法。假设某指标在 n 年内的数值分别为 V1, V2, ..., Vn,则年平均增长率 (r) 可以通过以下公式计算:
r = [(Vn / V1)^(1/n) - 1] × 100%
其中,Vn 表示最后一年(第n年)的数值,V1 表示第一年的数值,n 表示年份数量。
计算步骤:
1. 计算最终值与初始值的比率 (Vn / V1);
2. 将比率进行 n 次方根运算;
3. 从结果中减去 1;
4. 将结果乘以 100%,得到百分比形式的年平均增长率。
例如,某企业五年来的销售额分别为:100万,110万,120万,135万,150万。那么,其年平均增长率为:[(150/100)^(1/5) -1] × 100% ≈ 8.45%。这意味着企业销售额每年平均增长约 8.45%。
需要注意的是,几何平均法适用于计算增长率为正数的情况。如果增长率存在负数,则需要考虑使用其他方法,例如算术平均法,但算术平均法计算结果在某些情况下会失真。
不同类型数据的年平均增长率计算
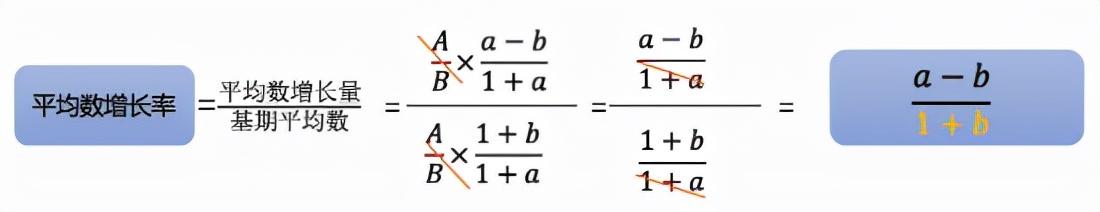
年平均增长率的计算方法在不同的数据类型中可能略有差异,需要根据数据的具体情况进行调整。例如,对于涉及人口增长或经济增长等连续型变量的数据,可以使用连续复利法进行更精确的计算。而对于离散型变量,例如企业销售额或利润等数据,则可以使用几何平均法。
此外,如果数据存在缺失值或异常值,需要进行必要的预处理,例如插值或去除异常值,以提高计算结果的准确性。在处理数据时,需要注意数据的可比性,例如货币单位、计量单位等因素需要保持一致,以确保计算结果的可靠性。选择合适的计算方法,并对数据进行必要的处理,对于获得准确的年平均增长率至关重要。
例如,在计算GDP增长率时,需要考虑通货膨胀的影响,通常会使用实际GDP增长率而非名义GDP增长率。 在计算某个产品销售量的年平均增长率时,需要考虑市场变化,季节性波动等因素,如果销售量存在大的波动,单纯使用几何平均法计算出的年平均增长率可能无法完全反映实际情况。
年平均增长率的应用及局限性分析
年平均增长率广泛应用于各个领域,例如:
* 经济学:衡量GDP、通货膨胀率、投资回报率等指标的增长情况;
* 财务管理:评估企业盈利能力、资产增长情况;
* 市场营销:分析市场规模、产品销量增长趋势;
* 人口统计:分析人口增长、预期寿命等指标。
然而,年平均增长率也存在一定的局限性:
* 它只反映了平均增长趋势,无法体现增长过程中的波动和变化;
* 它对极端值较为敏感,极端值可能会扭曲平均增长率;
* 它忽略了其他影响因素,例如政策变化、技术进步等。
因此,在使用年平均增长率时,需要结合其他指标和方法进行综合分析,才能更全面地了解增长情况。例如,可以使用标准差等指标来衡量增长率的波动性,或者结合其他因素进行多变量分析,以获得更全面的结论。
如何更准确地计算和解读年平均增长率
为了更准确地计算和解读年平均增长率,我们需要考虑以下几个方面:
首先,选择合适的计算方法至关重要。 前面提到的几何平均法适用于大多数情况,但如果数据存在负增长,或者需要考虑复合增长,则需要采用其他方法。
其次,数据质量直接影响计算结果的准确性。 数据的完整性、一致性和准确性都非常重要。 需要对异常值和缺失值进行处理,并确保数据的可比性。 例如,在计算物价指数的增长率时,需要考虑基期和权重的选择。
最后,在解读年平均增长率时,不能孤立地看待这个指标。 需要结合其他指标和信息进行综合分析,例如将年平均增长率与行业平均增长率进行比较,或者考虑宏观经济环境的影响等。 只有这样才能更全面、客观地理解数据,避免误解和偏差。

 鄂ICP备15020274号-1
鄂ICP备15020274号-1