本文详细阐述了正方体的体积计算公式a³,并深入分析了其在实际生活中的应用,例如包装设计和工程建设。文章还指出了计算中常见的误区,如单位换算错误和公式混淆,并展望了正方体体积计算的未来发展趋势。希望读者通过本文,能够熟练掌握正方体体积的计算方法,并避免计算错误。掌握正方体体积计算方法对于解决生活和工作中的实际问题至关重要,例如计算包装盒的容积和建筑材料用量。
正方体体积计算公式及推导
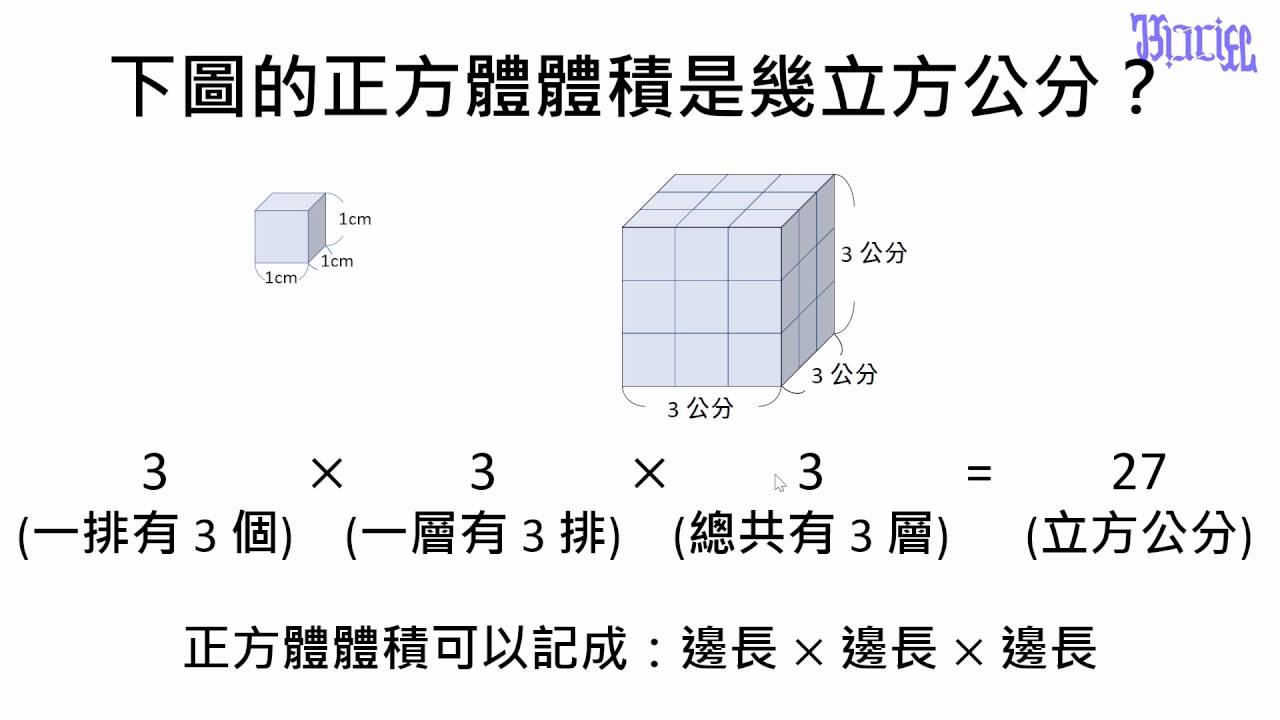
正方体的体积计算是几何学中的基础知识,其公式简单易懂,但理解其推导过程有助于更深刻地掌握这一概念。正方体,顾名思义,具有六个完全相同的正方形面,所有棱长都相等。假设正方体的棱长为a,我们可以将正方体想象成由许多个相同的小正方体堆叠而成。我们可以先考虑一个棱长为a的正方体底面,其面积为a*a = a²。然后,将无数个与底面相同的正方形面沿着垂直方向堆叠,高度也是a,这样就形成了一个棱长为a的正方体。因此,正方体的体积V可以表示为底面积乘以高,即V = a² * a = a³。这个公式简洁明了,是所有正方体体积计算的基础。
理解了这个公式的推导,我们就能更好地理解为什么正方体的体积只与棱长有关,并且是棱长的三次方。这意味着如果棱长加倍,体积将增加到原来的八倍。例如,一个棱长为2厘米的正方体,其体积为2³ = 8立方厘米;而棱长为4厘米的正方体,体积则为4³ = 64立方厘米。这个简单的公式在日常生活中以及各种工程计算中都具有广泛的应用。
正方体体积计算在实际生活中的应用
正方体体积的计算并非仅仅是数学理论上的概念,它在实际生活中有着广泛的应用。例如,在包装设计中,我们需要计算包装盒的容积,以确定包装盒的大小是否能够容纳商品。假设我们需要设计一个正方体形状的包装盒来包装一个体积为1000立方厘米的商品,那么我们需要计算出包装盒的棱长。根据公式a³=V,我们可以计算出a=∛1000=10厘米,因此包装盒的棱长至少需要10厘米。
另一个常见的应用场景是工程建设。在建筑工程中,我们常常需要计算各种构件的体积,例如混凝土浇筑量、砖块用量等。假设我们需要计算一个正方体形状的混凝土基础的体积,已知其棱长为2米,那么其体积为2³=8立方米。这有助于我们精确地估算所需的建筑材料数量,进而控制工程成本。这些例子都充分说明了正方体体积计算在实际生活中的重要作用。
正方体体积计算中的常见误区及注意事项
- 单位换算错误:在进行正方体体积计算时,一定要注意单位的一致性。例如,如果棱长单位是厘米,那么体积单位就是立方厘米;如果棱长单位是米,那么体积单位就是立方米。单位换算错误是导致计算结果错误的常见原因。
- 公式混淆:有些同学可能会将正方体的体积公式与正方体的表面积公式混淆,导致计算结果出错。正方体的表面积公式为6a²,而体积公式为a³,两者计算结果完全不同。
- 小数点计算错误:在进行小数点计算时,一定要细心,避免出现小数点计算错误。尤其是在棱长为小数时,小数点计算错误很容易导致计算结果出现很大的偏差。
- 忽略实际情况:在实际应用中,正方体的体积计算需要结合实际情况进行。例如,在计算包装盒的体积时,需要考虑包装材料的厚度;在计算混凝土基础的体积时,需要考虑混凝土的收缩率。
- 维度理解错误:正方体的体积是三维的,其单位是立方单位,而不是平面单位。一些同学可能会误以为正方体的体积是其棱长的平方,这是一个常见的误区。
正方体体积计算的未来发展及展望
随着科技的发展,正方体体积计算的方法也将会不断发展和完善。例如,计算机技术和人工智能技术的应用,使得正方体体积的计算更加自动化和高效。一些三维建模软件可以自动计算出复杂形状物体的体积,其中也包括正方体。
此外,在一些特殊领域,例如纳米技术,对正方体体积的计算精度要求也越来越高。这将推动相关计算方法和技术的不断改进和创新。未来,我们可能会有更精确、更快速的正方体体积计算方法出现,这些方法将会在各个领域发挥更大的作用。 例如,在未来更精确的测量技术下,对正方体棱长的测量精度更高,计算出的体积也就更精准。而人工智能的介入,能够让计算过程自动化并减少人为错误。




 鄂ICP备15020274号-1
鄂ICP备15020274号-1