本文详细讲解了长方形体积(长方体体积)的计算方法,从基础公式到应对不规则形状的技巧,并结合生活实际案例分析了其应用,最后探讨了该计算方法的未来发展趋势,涵盖长方体体积计算公式、不规则长方体体积计算等长尾关键词。
长方体体积计算公式:基础篇
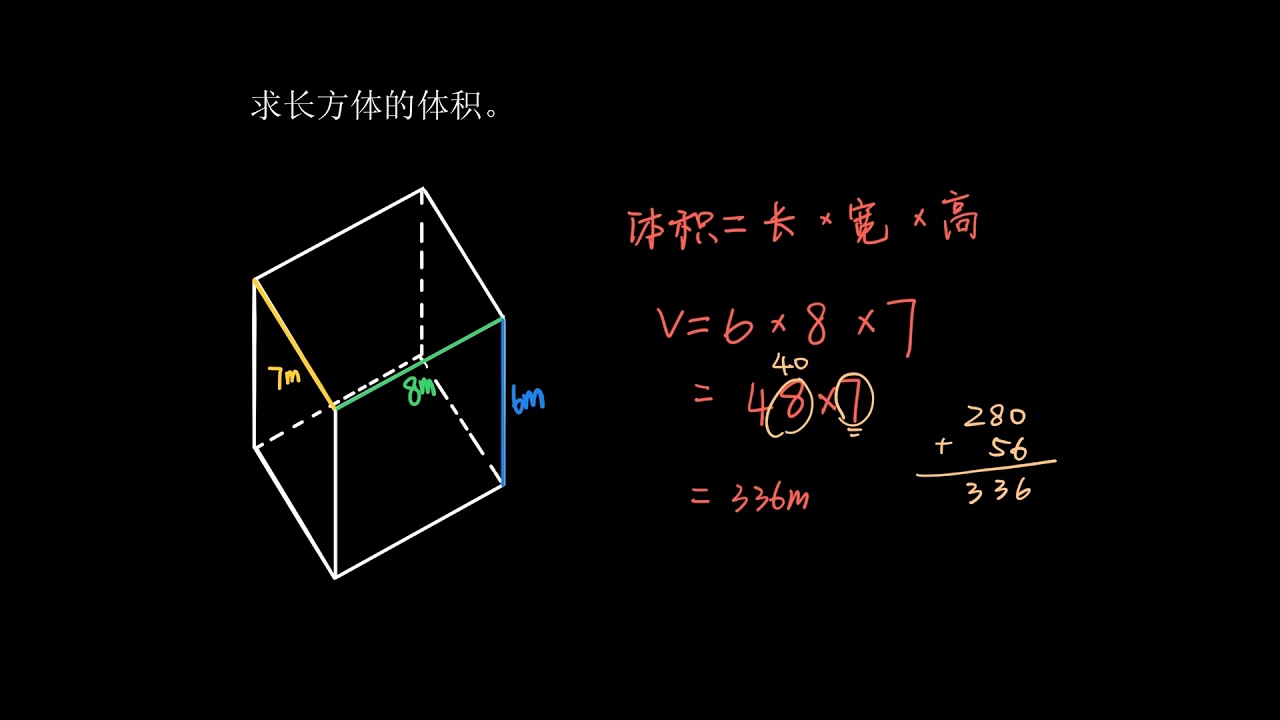
长方体的体积计算是几何学中的基础知识,也是生活中经常用到的实用技能。长方体的体积,简单来说,就是它所占据空间的大小。计算长方体体积最常用的公式是:体积 = 长 × 宽 × 高。
这个公式的理解非常直观。我们可以想象一下,一个长方体是由许多个小正方体堆积而成的。如果长方体的长是 a,宽是 b,高是 c,那么它的体积就是 a × b × c 个小正方体的体积之和。
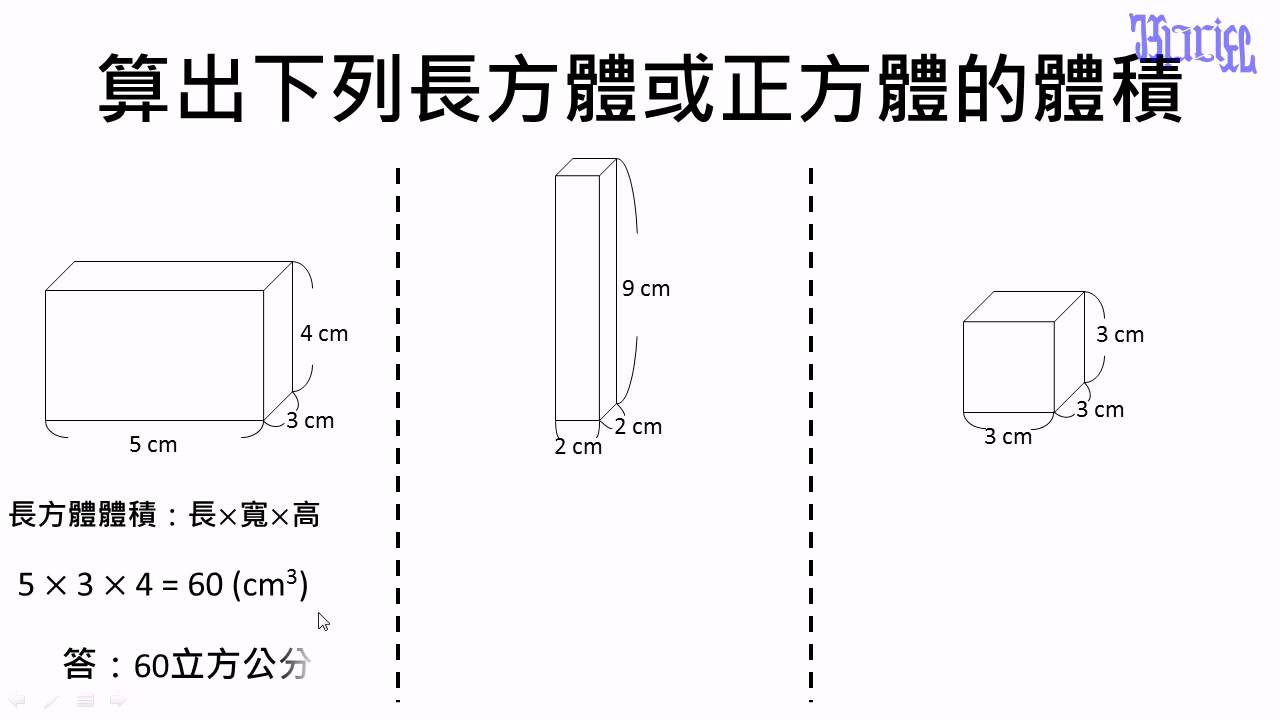
例如,一个长 5 厘米,宽 3 厘米,高 2 厘米的长方体,它的体积就是 5 × 3 × 2 = 30 立方厘米。这个公式适用于所有规则的长方体,无论是包装箱、储物柜,还是建筑物中的房间,只要其长、宽、高都已知,就可以轻松计算出它的体积。
在实际应用中,我们需要根据具体情况选择合适的单位。例如,计算房间体积时,通常使用立方米;计算包装盒体积时,通常使用立方厘米或立方分米。单位的换算也需要掌握,例如1立方米 = 1000000立方厘米。
长方体体积计算公式:进阶篇——应对不规则形状
实际生活中,我们有时会遇到形状不规则的长方体,例如一些被切割过的木块或石块。对于这类情况,简单的长×宽×高公式就无法直接应用了。这时,我们需要根据实际情况进行分割或变形,将其分解成若干个规则的长方体,分别计算每个规则长方体的体积,再将各个部分的体积加起来,得到整个不规则长方体的体积。
例如,一个被切割成两部分的不规则长方体,我们可以将其分成两个规则的长方体,分别计算它们的体积,再相加得到整体体积。这需要我们具备一定的空间想象能力和几何分析能力。
另外,一些特殊形状的长方体,其长、宽、高可能并非垂直方向的边长。例如,一个倾斜的长方体,我们需要先将其分解成规则的长方体再进行计算。 这需要我们灵活运用几何知识,进行巧妙的分割和计算,这部分计算需要结合具体的几何知识进行处理。一些复杂形状的体积计算,可能需要借助积分等高等数学工具。
长方体体积计算在生活中的应用
长方体体积的计算在日常生活中有着广泛的应用,例如:
1. **购物:** 购买包装材料,如纸箱、塑料盒等,需要根据物品的体积选择合适的包装尺寸。这时就需要运用长方体体积计算公式,确保物品能够完全被包装住。如果包装过大则会浪费资源,如果包装过小则会造成损坏。
2. **装修:** 装修房屋时,需要计算房间的体积,以便估算所需的涂料、地板等材料的数量,避免材料浪费和短缺。这部分需要精准计算才能控制成本。
3. **物流:** 在物流行业中,需要计算货物的体积,以便安排合适的运输工具和路线,提高运输效率。体积计算的精准度直接影响运输成本和效率。
4. **土方工程:** 土方工程中,需要计算土石方的体积,以便确定工程量,制定施工计划。准确的体积计算,可以确保工程顺利进行。
5. **农业:** 计算仓库或储藏室的容积,以便估算可以存储的粮食或农产品的数量。这有助于农业生产的规划。
长方体体积计算的单位换算与精度问题
在进行长方体体积计算时,单位的选取和换算非常重要,不同的单位对应不同的计算结果。例如,计算一个长方体储物柜的体积时,我们需要根据实际情况选择合适的单位,如立方米或立方厘米。如果单位选取错误,计算结果就会出现偏差。
此外,在实际测量中,由于测量工具和方法的限制,会产生一定的误差。因此,我们需要尽可能提高测量的精度,以减少计算误差。
例如,使用精度更高的测量工具,例如游标卡尺或激光测距仪,可以提高测量的精确度。
在工程计算中,我们往往需要考虑误差范围,避免因误差导致的工程事故。因此,工程计算中的精度问题显得尤为重要。
为了保证计算的精度,在实际计算中,我们可以采用多次测量取平均值的方法来减少测量误差。
同时,我们需要根据实际情况选择合适的精度,过高的精度追求会增加计算的复杂度,而过低的精度则会影响计算结果的准确性。
长方体体积计算的未来发展趋势
随着科技的不断进步,长方体体积的计算方法也在不断发展。例如,三维扫描技术可以快速准确地获取物体的三维模型,然后通过计算机软件计算出物体的体积。这比传统的测量方法更加高效和精确。
人工智能技术也可以应用于长方体体积计算,例如通过图像识别技术自动识别物体的形状和尺寸,然后计算出其体积。这将大大提高计算效率和自动化程度。
未来,长方体体积计算可能会与其他技术结合,例如与物联网技术结合,实现对物体的实时体积监测。这将为各个行业带来更多的应用和便利。例如,在物流行业,可以实时监测货物的体积,优化运输方案。
总的来说,长方体体积计算技术的未来发展趋势是更加智能化、自动化和高效化。

 鄂ICP备15020274号-1
鄂ICP备15020274号-1