三角函数怎么求？深度解析三角函数计算方法及应用场景

本文详细讲解了三角函数怎么求，从三角函数的定义、特殊角三角函数值的记忆、计算器的辅助应用到实际应用场景分析，以及误差分析和挑战，力求帮助读者全面掌握三角函数计算方法和技巧，并能够在实际问题中灵活运用。学习三角函数计算不仅需要掌握公式，更要理解其背后的原理和应用，才能真正学以致用。

理解三角函数定义：从单位圆到公式推导

要理解三角函数怎么求，首先必须明确三角函数的定义。在数学中，三角函数是描述直角三角形中角与边的关系的函数，包括正弦（sin）、余弦（cos）、正切（tan）等。

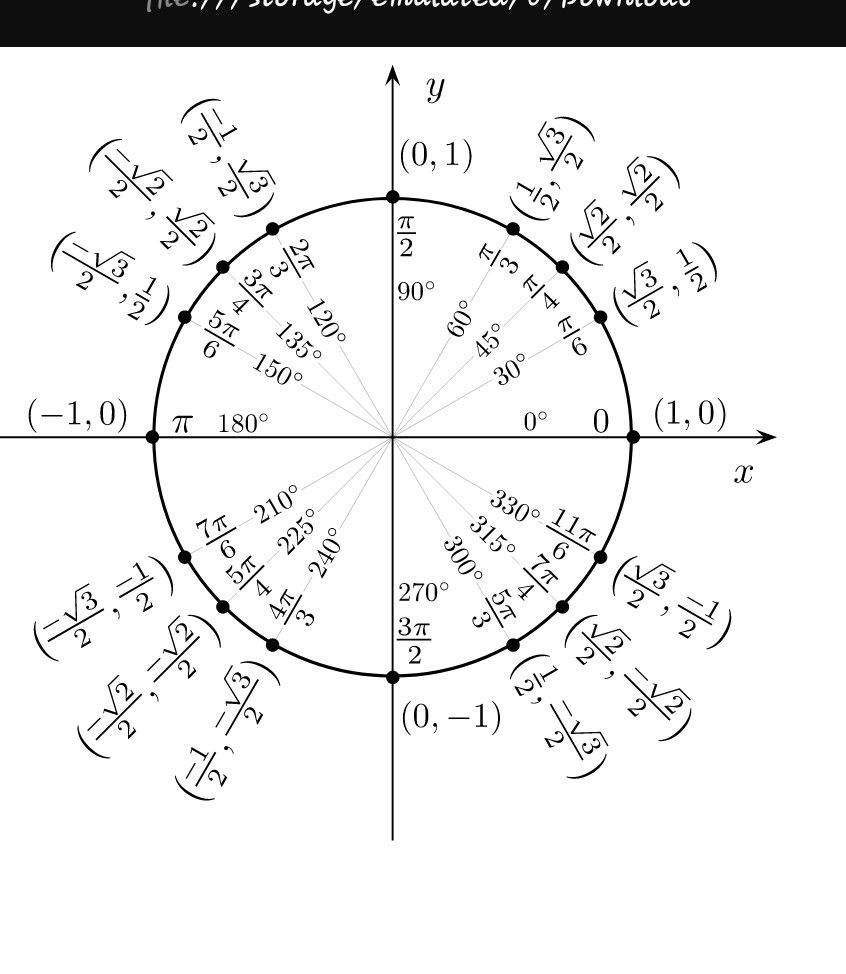
一个更通用的理解方式是基于单位圆。单位圆是一个半径为 1 的圆。在单位圆上，任意一个角 θ 可以与圆周上一点 (x, y) 对应。

根据定义，该点的 x 坐标即为角 θ 的余弦值 cos(θ)，y 坐标即为角 θ 的正弦值 sin(θ)。正切值 tan(θ) 则定义为 sin(θ) / cos(θ)。

从单位圆定义出发，可以推导出各种三角函数公式，例如：勾股定理的三角函数形式：sin²θ + cos²θ = 1，以及其他一些重要的恒等式，这些公式是进行三角函数计算的重要工具。

例如，已知一个角的正弦值，我们可以利用 sin²θ + cos²θ = 1 来计算它的余弦值。掌握这些基础定义和公式，是求解三角函数的关键第一步。

掌握特殊角三角函数值：快速计算的关键

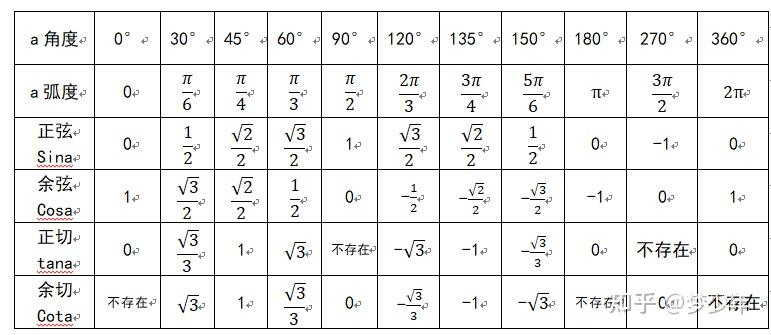
在实际计算中，一些特殊角度的三角函数值经常被用到，例如 0°、30°、45°、60°、90° 等。熟记这些特殊角的三角函数值，可以极大地提高计算效率。

例如，sin 30° = 1/2，cos 60° = 1/2，tan 45° = 1 等。这些数值可以通过单位圆或直角三角形的特殊比例关系得到。

很多三角函数的计算题中，都包含了特殊角的变形。例如，一个角度可能可以通过角的和差公式化简为特殊角的组合。

熟练掌握这些特殊角三角函数值，并能够熟练运用三角函数公式进行变形，是提高三角函数计算速度的关键。 这也让一些复杂的计算问题可以简化成简单易算的特殊角情况。

因此，记住这些特殊值及其变形，并能灵活运用是高效掌握三角函数计算的关键。

三角函数计算器与软件：辅助计算工具

虽然掌握三角函数的定义和公式非常重要，但对于一些复杂的三角函数计算，使用计算器或专业的数学软件可以提高效率并减少错误。

现在有很多科学计算器和数学软件，如MATLAB、Python中的NumPy库等，可以直接计算三角函数的值。

这些工具可以处理各种角度的三角函数计算，包括角度单位的转换（度和弧度）。

此外，一些计算器和软件还具有绘图功能，可以帮助我们理解三角函数图像，从而更直观地理解三角函数的变化规律。

值得注意的是，过分依赖计算器会降低对三角函数公式和基本概念的理解，因此，在学习初期，应尽量多进行手工计算，只有在确认掌握了基础知识后，才能合理地借助工具。

三角函数在实际生活中的应用：从工程到自然科学

三角函数并非仅仅是数学概念，它在工程、物理、计算机科学等诸多领域都有广泛的应用。

例如，在工程测量中，三角函数用于计算距离、高度、角度等。在建筑工程中，三角函数可以用于计算建筑物的倾斜角度和结构稳定性。

在物理学中，三角函数用于描述波的运动、振动现象、以及许多力学问题中的向量分解和合成，例如简单谐振动的分析等。

在计算机图形学中，三角函数用于坐标变换，三维建模，以及其他各种图形渲染相关的计算，例如动画制作。

总之，三角函数是许多科学和工程问题的基础，熟练掌握它的计算方法，才能在这些领域更好地应用数学知识解决实际问题。

三角函数计算的误差分析与挑战：提高计算精度的方法

在实际应用中，由于测量误差、计算方法的近似性等原因，三角函数的计算结果可能存在一定的误差。

例如，使用近似公式计算三角函数值时，角度越偏离特殊角，误差越大。

为了提高计算精度，需要选择合适的计算方法，例如使用泰勒展开式等高级算法进行计算。

此外，还可以通过多次测量取平均值来减小测量误差的影响。

深入理解三角函数计算的误差来源，并采取相应的措施来减少误差，是保证计算结果准确性的关键。 在实际应用中，要充分考虑误差对结果的影响，并采取合适的应对措施。