轻松掌握中位数计算方法：从入门到精通，数据分析不再难

清风明月夜 2024-12-24 热点榜单 706 次浏览 0个评论

本文详细讲解了中位数的计算方法，涵盖了奇数和偶数个数数据集的处理方法，并深入探讨了中位数的优缺点以及在数据分析中的应用和未来发展趋势。通过学习本文，读者可以轻松掌握中位数计算，并在实际工作中灵活应用，提升数据分析能力，解决例如如何计算奇数个数数据集中位数或如何计算偶数个数数据集中位数等问题。

理解中位数：数据排序与位置的重要性

中位数，顾名思义，是指将一组数据按照大小顺序排列后，位于中间位置的数值。理解中位数的关键在于『排序』和『中间位置』。

首先，我们需要将数据进行排序，从小到大或从大到小，这步至关重要，因为它决定了中位数的准确位置。排序完成后，我们就能够轻松找到中位数。

数据的个数会影响中位数的求法。如果数据个数是奇数，中位数就是排序后位于中间位置的数值；如果数据个数是偶数，中位数就是中间两个数值的平均数。

例如：数据集合{3, 1, 4, 1, 5, 9, 2, 6, 5}，排序后为{1, 1, 2, 3, 4, 5, 5, 6, 9}，个数为9（奇数），中位数为4。而数据集合{2, 4, 6, 8}排序后为{2, 4, 6, 8}，个数为4（偶数），中位数为(4+6)/2=5。

掌握这个基本原理，就能轻松计算出大部分数据的中位数。

当数据个数为奇数时，求中位数相对简单。只需将数据从小到大排序，然后直接找到处于中间位置的数值即可。这个数值就是中位数。

例如，有一组学生考试成绩：78, 85, 92, 75, 88, 95, 82。我们先将这些成绩从小到大排序：75, 78, 82, 85, 88, 92, 95。这组数据共有7个，中间位置的数值是第(7+1)/2 = 4个，因此，中位数是85分。

需要注意的是，在实际应用中，可能会遇到大量数据，人工排序耗时费力。这时，我们可以借助计算机软件或编程工具进行排序，提高效率，避免计算错误。一些统计软件包，例如SPSS,R,Python的pandas库等，都内置了计算中位数的函数，可以快速处理大量数据。

当数据个数为偶数时，中位数的计算稍有不同。需要先将数据排序，然后取中间两个数的平均值作为中位数。

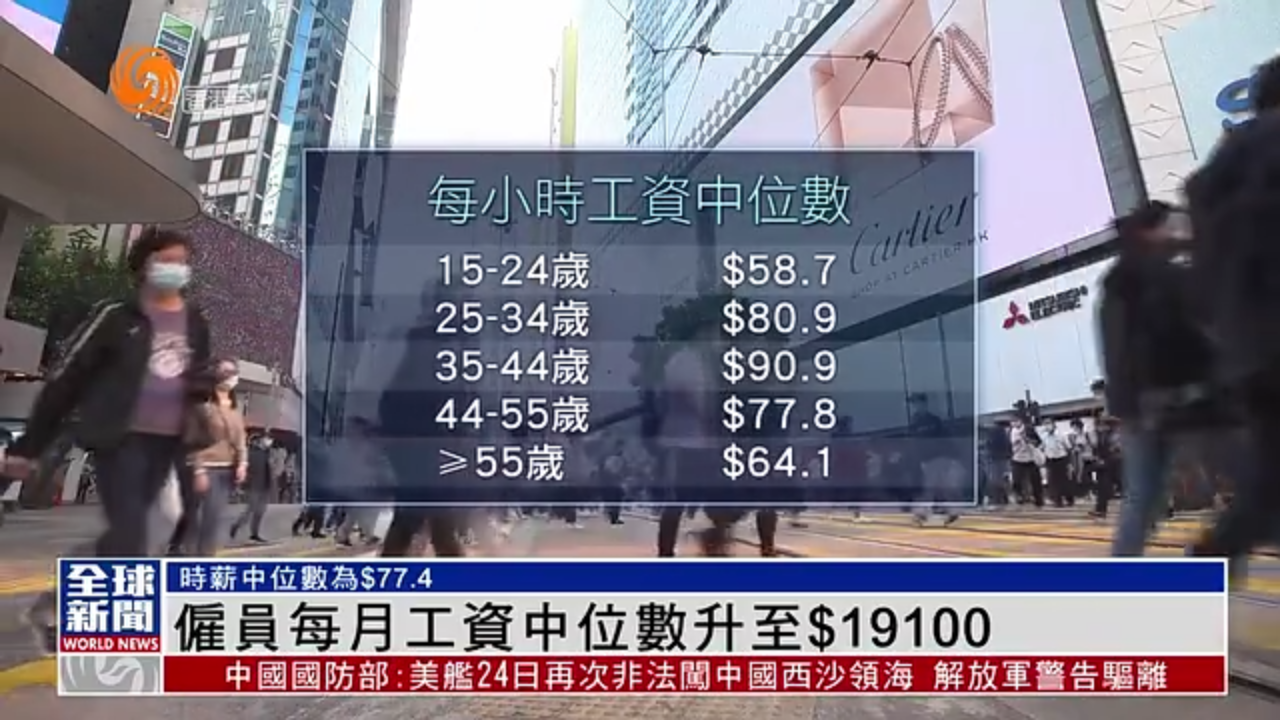
例如，某公司员工的月薪数据为：5000, 6000, 7000, 8000。排序后为：5000, 6000, 7000, 8000。数据个数为4，中间两个数是6000和7000，中位数为(6000+7000)/2 = 6500元。

同样，对于大规模数据的处理，计算机软件或编程工具可以极大地方便计算过程，避免人工计算可能出现的错误。准确地计算中位数对于工资水平的统计分析，以及其他许多领域的数据分析都是至关重要的。

中位数不受极端值的影响，更能反映数据的集中趋势，避免个别极端值扭曲结果。例如，计算一组收入数据的中位数时，如果其中存在少数高收入者，中位数仍然能够反映大部分人的收入水平。
中位数的计算相对简单，易于理解和掌握。即使没有很强的数学基础，也能轻松学会计算中位数。
中位数在描述偏态分布数据时，比平均数更具有代表性。当数据集中存在极端值时，使用中位数比平均数更能准确地反映数据的集中趋势。
中位数广泛应用于各个领域，例如统计学、经济学、社会学等。在数据分析中，中位数是一个重要的统计量，可以用来描述数据的集中趋势。
中位数计算方便，无需进行复杂的计算，对于初学者来说非常友好，更容易理解和应用。尤其在大数据时代，处理大量数据时，中位数的计算效率更高效。