百分位数怎么算？深度解析及应用场景详解

本文详细阐述了百分位数的计算方法，特别是线性插值法，并通过多个实际案例分析了百分位数在金融、教育和医疗等领域的应用。文章还探讨了百分位数计算的潜在挑战和未来发展方向，例如数据量过大时的计算效率问题以及如何结合其他统计指标进行更深入的分析。希望本文能够帮助读者更好地理解和应用百分位数这一重要的统计工具。

理解百分位数的概念及其意义

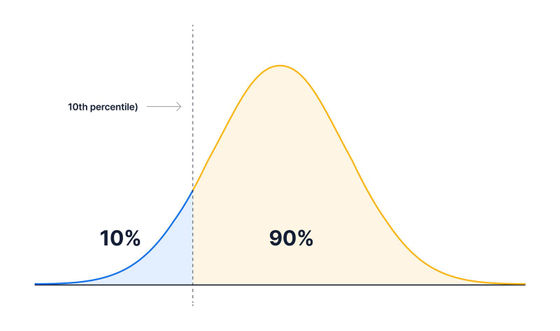
百分位数，简单来说，就是将一组数据从小到大排列后，按百分比划分出来的数值。例如，第90百分位数表示有90%的数据小于或等于这个数值。理解百分位数的关键在于明白它是一种相对位置的度量，而非绝对值。它能够有效地反映数据的分布情况，尤其是在数据量较大、分布不均匀的情况下，百分位数比平均数更能直观地展现数据特征。

举例来说，如果一个班级的数学考试成绩的第75百分位数是85分，这意味着有75%的学生的成绩在85分或以下。这比单纯知道平均分更有意义，因为它告诉我们成绩分布的整体情况。

百分位数在统计学和数据分析中应用广泛，它能帮助我们理解和分析不同群体或样本的数据分布特征，并以此作出相应的决策。例如，在医疗领域，医生可以利用百分位数来评估婴儿的身高体重是否达标；在教育领域，教师可以利用百分位数来了解学生的学习成绩在班级中的相对位置。

百分位数的计算方法：线性插值法

百分位数的计算方法有很多种，其中线性插值法最为常用。这种方法基于对数据排序后的位置进行计算，公式较为简单，易于理解和应用。首先，需要将数据从小到大排序。然后，根据所需百分位数P，计算其在排序数据中的位置：位置 = (P/100) * (n + 1)，其中n是数据个数。如果位置是整数，则该位置对应的数值就是P百分位数；如果位置是小数，则需要进行线性插值。线性插值是指在两个相邻数据点之间进行加权平均，权重由小数部分决定。

例如，计算一组数据{2, 5, 7, 10, 12}的第70百分位数。首先，将数据排序，然后计算位置：(70/100) * (5 + 1) = 4.2。由于位置不是整数，需要进行线性插值：第70百分位数 = 第4个数据 + 0.2 * (第5个数据 - 第4个数据) = 10 + 0.2 * (12 - 10) = 10.4。

需要注意的是，不同的计算方法可能得到略微不同的结果，这取决于采用的算法和插值方法。在实际应用中，选择合适的计算方法需要根据数据的具体情况和分析目的而定。

百分位数在不同领域的应用案例

百分位数的应用范围非常广泛，几乎涵盖了各个领域。在金融领域，百分位数常用于风险管理，例如计算投资组合的VaR(Value at Risk)，即在一定置信水平下，投资组合在未来一段时间内可能遭受的最大损失。

在教育领域，百分位数可以用于评价学生的考试成绩，例如将学生的成绩与全国或省级的同龄学生进行比较，从而了解学生的学习水平在全国或全省的相对位置，以便进行有针对性的教学。

在医疗领域，百分位数用于评估婴儿的生长发育情况，例如根据婴儿的身高、体重等数据计算其百分位数，判断婴儿是否处于正常的生长发育范围内。这些案例充分展示了百分位数在不同领域中的应用价值和广泛性。

此外，百分位数还可以用于质量控制，例如计算产品的某个指标的百分位数，判断产品质量是否达标。总的来说，百分位数是一种强大的统计工具，可以帮助我们更好地理解和分析数据，做出更明智的决策。

百分位数计算的潜在挑战与未来发展

• 数据量过大时的计算效率问题
• 不同计算方法结果的差异性分析
• 异常值对百分位数的影响及处理
• 百分位数应用中的误解及防范
• 百分位数与其他统计指标的结合应用