平行四边形的面积怎么算？详解公式、推导及应用场景

本文详细阐述了平行四边形的面积计算方法，从公式推导、不同类型平行四边形的计算以及实际应用等方面进行了深入探讨，并指出了该公式的局限性以及未来发展趋势。掌握平行四边形面积计算不仅对学习几何知识至关重要，更能在实际生活中解决诸多问题，例如土地测量、建筑工程等。理解‘底’与‘高’的概念，并灵活运用不同计算方法，是熟练掌握平行四边形面积计算的关键。

平行四边形面积计算公式及推导

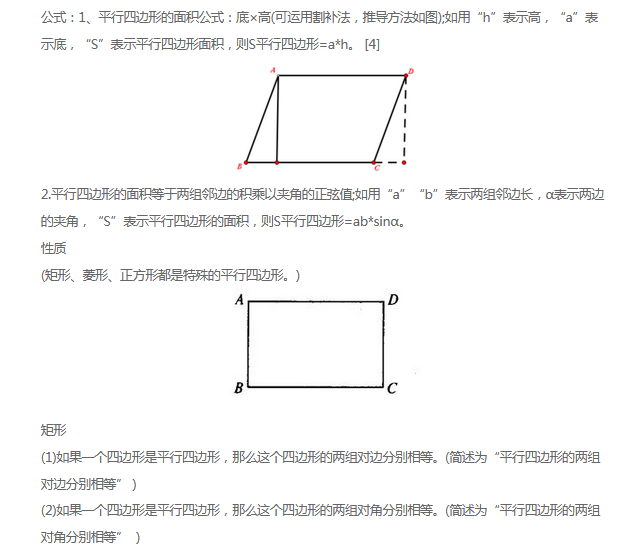
平行四边形的面积计算是平面几何中的基础知识点，其核心公式为：面积 = 底 × 高。

理解这个公式的关键在于明确‘底’和‘高’的含义。‘底’指的是平行四边形任意一边的长度；而‘高’指的是从底边上的一点到对边作垂线，垂线段的长度就是高。

那么，这个公式是如何推导出来的呢？我们可以通过将平行四边形转化为长方形来理解。想象一下，我们从平行四边形的一侧剪下一个三角形，并将这个三角形移动到平行四边形的另一侧。这时，你会发现，原本的平行四边形变成了一个长方形！长方形的面积很容易计算，就是长乘以宽。而这个长方形的长就是平行四边形的底，宽就是平行四边形的高。因此，平行四边形的面积就等于底乘以高。

举个例子：一个平行四边形的底是 5cm，高是 3cm，那么它的面积就是 5cm × 3cm = 15cm²。

这个公式的推导过程清晰地展现了数学中化归思想的魅力，将一个看似复杂的问题转化为简单的、已知解法的问题，从而轻松解决。

不同类型平行四边形面积的计算

虽然平行四边形面积计算的通用公式是面积 = 底 × 高，但在实际应用中，我们可能会遇到各种不同类型的平行四边形，例如正方形、菱形等。

对于正方形来说，因为它的底和高都相等，所以面积计算就简化为边长 × 边长。而对于菱形，它的面积计算公式可以表示为：面积 = (对角线1 × 对角线2) / 2。这个公式可以从将菱形分割成两个全等的三角形推导出来。

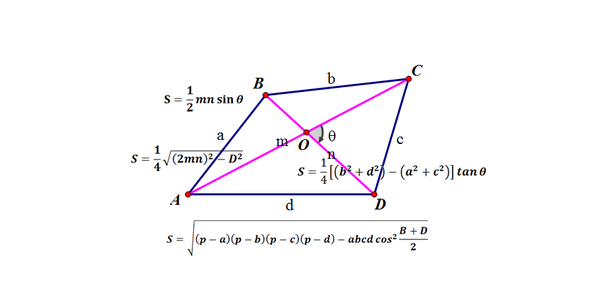
此外，还有一些不规则的平行四边形，其底和高的测量可能需要更复杂的几何方法。例如，如果我们只知道平行四边形的两条邻边和夹角，那么我们可以利用三角函数计算出高，再应用面积公式计算面积。

不同的平行四边形类型，计算方法略有差异，但其本质都是基于面积=底×高这一核心公式。选择合适的计算方法取决于所掌握的已知条件。

平行四边形面积计算在实际生活中的应用

• 测量土地面积：在农业生产、土地规划等领域，经常需要计算不规则土地的面积。将不规则土地分割成多个平行四边形，分别计算面积，然后加总，就可以得到总面积。
• 建筑工程：建筑设计中，平行四边形结构被广泛应用，例如屋顶设计，需要计算屋顶的面积来确定所需材料的数量。
• 艺术设计：在图案设计、平面设计等领域，平行四边形元素被大量应用，例如某些瓷砖的设计就是基于平行四边形。设计师需要计算平行四边形的面积，才能进行相应的尺寸调整和布局设计。
• 物理学中的应用：在某些力学计算中，平行四边形法则用于矢量合成与分解，通过计算平行四边形的面积来推算相关物理量。
• 包装设计：一些商品包装，例如礼盒，可能会用到平行四边形的结构，这需要精确计算包装盒的用料，以达到最佳的成本效益。

平行四边形面积计算公式的局限性及未来发展

虽然平行四边形面积计算公式简单实用，但它也存在一些局限性。

首先，该公式只适用于平面几何中的平行四边形。对于三维空间中的平行六面体等立体图形，则需要采用不同的计算方法。

其次，在实际测量中，获得精确的底和高数据可能存在一定的误差，这会影响最终计算结果的精度。

在未来，随着计算机技术的不断发展，我们可以利用更先进的计算机辅助设计（CAD）软件和三维扫描技术，更精确地测量和计算不规则形状的面积。人工智能技术也能被用于更高效、更精准地计算平行四边形的面积。

此外，对于一些特殊的平行四边形，例如底边和高难以直接测量的情况，需要开发更有效的计算方法，例如运用坐标系计算面积等，从而提升计算效率和准确度。