平行四边形的高怎么求？详解各种求高方法及应用场景

本文详细阐述了平行四边形的高的求法，从定义、不同方法到实际应用及挑战，全面解析了平行四边形高计算的各个方面，并结合多个实际案例进行分析，读者可以轻松掌握平行四边形的高怎么求，并应用于实际问题中，例如利用三角函数求平行四边形的高或已知面积求高。

理解平行四边形的高：定义与意义

平行四边形的高，指的是从平行四边形的一个顶点向其对边（或对边的延长线）作垂线，垂线段的长度就是平行四边形的高。理解平行四边形的定义至关重要，它是一个两组对边分别平行的四边形。而高，则是计算平行四边形面积的关键要素。

求平行四边形的高，在几何计算中具有重要意义，它直接关系到面积的计算。准确求出高，才能准确计算出平行四边形的面积，这在工程测量、建筑设计、乃至日常生活中的面积计算中都有广泛的应用。例如，计算一块不规则形状的田地面积时，可以将其分割成多个平行四边形，然后分别计算每个平行四边形的面积，最终得到总面积。

此外，理解平行四边形的高也为后续学习更复杂的几何图形打下基础。例如，学习三角形、梯形等图形的面积计算，也需要运用到类似的垂直高度的概念。因此，掌握平行四边形的高的求法是学习几何知识的重要基础。

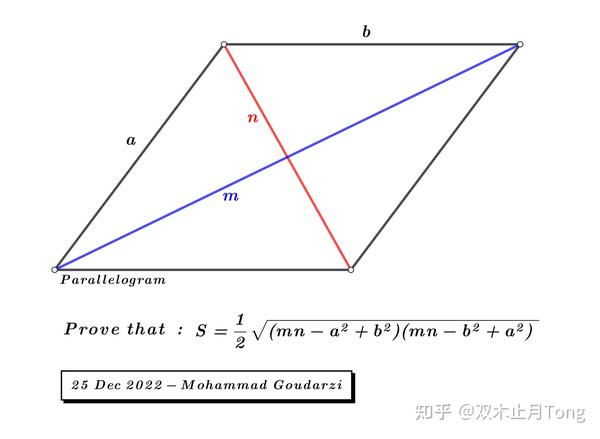
不同类型平行四边形的求高方法

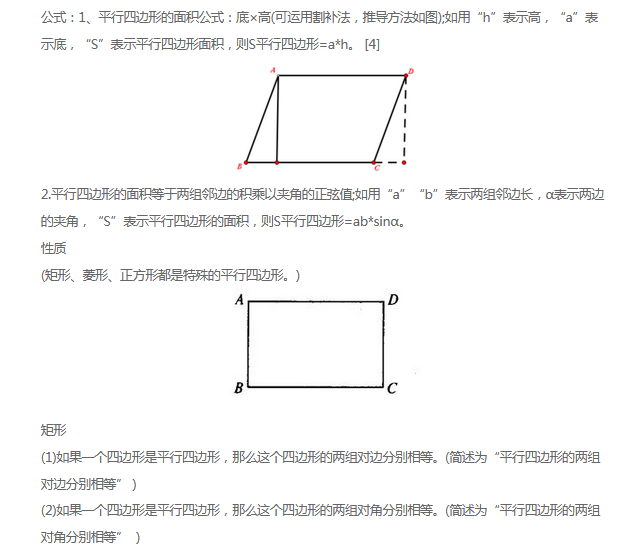
根据已知条件的不同，求平行四边形的高的方法也各不相同。如果已知平行四边形的底和面积，则高可以直接通过公式：高 = 面积 ÷ 底计算得出。例如，一个平行四边形的面积为 24 平方厘米，底为 6 厘米，则高为 24 ÷ 6 = 4 厘米。

如果已知平行四边形的两条邻边和它们之间的夹角，则可以使用三角函数知识求高。例如，已知两邻边长分别为 a 和 b，夹角为 θ，则高 h 可以通过公式 h = b * sinθ 计算。 这时，需要用到三角函数中的正弦函数。这在实际应用中，当我们无法直接测量高的时候，可以通过测量邻边和夹角来间接计算高。

还有一种情况是已知平行四边形的四个顶点的坐标，这时可以用坐标方法计算高。通过两点间的距离公式和点到直线的距离公式，可以计算出平行四边形的底边和对应顶点到底边的距离，这个距离也就是平行四边形的高。这需要一定的解析几何知识。

利用三角函数求解平行四边形的高

• 方法一：利用正弦函数。已知平行四边形的底边长和一个内角，就可以利用正弦函数计算出高。公式为：高 = 邻边长 × sin(角度)。
• 方法二：利用余弦定理。如果已知平行四边形的两条邻边及夹角，可以利用余弦定理计算出对角线的长度，再通过三角形面积公式求出高。
• 方法三：通过构建直角三角形。我们可以从平行四边形顶点向底作垂线，形成一个直角三角形。如果已知斜边和一个锐角，就可以利用三角函数求出高。
• 方法四：利用勾股定理。当平行四边形是矩形或正方形时，可以利用勾股定理来求高。因为矩形和正方形的高就是其边长。
• 方法五：在一些特殊情况下，如菱形，利用其对角线互相垂直平分性质，可简化求高过程。我们可以直接利用对角线和底边计算出高。

平行四边形高求解的实际应用与案例分析

在实际生活中，求平行四边形的高有着广泛的应用。例如，在土木工程中，计算房屋屋顶的面积时，通常会将屋顶简化成平行四边形模型，此时就需要计算平行四边形的高来求得屋顶面积。根据建筑图纸上提供的尺寸数据，工程师们就可以运用相关的几何知识计算出屋顶的高度，从而计算出屋顶的面积，进而确定所需要的建筑材料。

在农业生产中，计算田地面积时，如果田地形状接近平行四边形，也可以通过测量田地的底边和高来计算田地的面积。这对于农民朋友来说至关重要，这直接关系到他们农作物种植规划，以及化肥用量等。

此外，在艺术设计、服装设计等领域，求平行四边形的高也能发挥作用。例如，在设计一些具有平行四边形图案的装饰品或服装时，设计师需要精确计算平行四边形的高来保证图案的比例和谐。

平行四边形高求解的误区与挑战

在求解平行四边形的高的过程中，也存在一些常见的误区。一些同学容易将平行四边形的任意一边都当作底边，而忘记了高是垂直于底边的垂线段。这种误解会导致计算结果出错。

此外，在实际测量中，由于测量工具的精度限制以及人为误差的存在，可能会导致测量数据存在偏差，从而影响最终计算结果的准确性。因此，在进行测量时，需要注意提高测量精度，并进行多次测量取平均值，以减小误差的影响。

对于一些形状不规则的平行四边形，直接测量其高比较困难。这时，需要采用间接测量的方法，例如利用三角函数或坐标法进行计算。这需要一定的数学知识和计算能力。