梯形的高怎么求？详解梯形面积计算及多种求高方法

本文系统地介绍了如何求梯形的高，详细阐述了利用梯形面积公式、已知梯形周长和对角线求高、利用坐标法求高以及特殊梯形求高的方法。文章结合实际案例，分析了各种方法的优缺点，并对未来梯形高计算的发展趋势进行了展望，希望能够帮助读者全面理解和掌握梯形高计算技巧，并能够根据不同的已知条件选择最合适的方法。

利用梯形面积公式求高

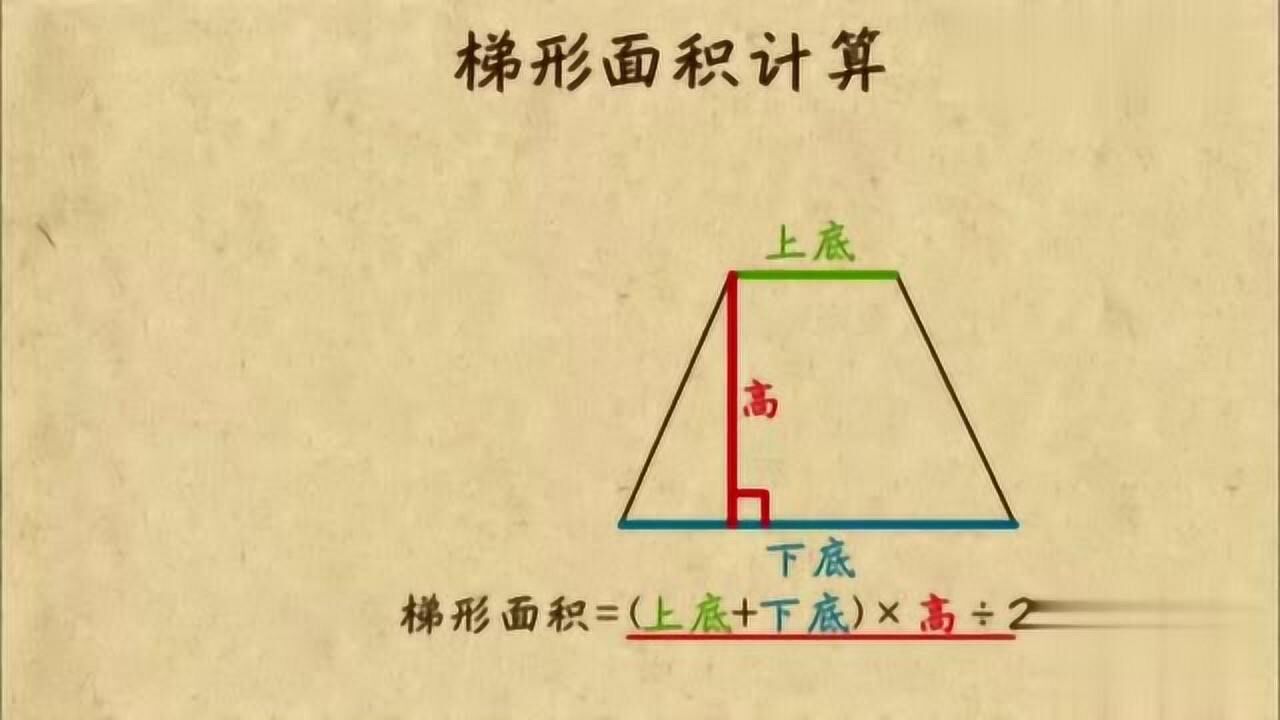
求梯形的高，最基础也是最常用的方法是利用梯形面积公式。梯形面积公式为：S = (a+b)h/2，其中S表示梯形面积，a和b分别表示梯形的上下底长，h表示梯形的高。

如果已知梯形的面积S和上下底长a、b，则可以很容易地求出梯形的高h：h = 2S/(a+b)。

例如，一个梯形的面积为60平方厘米，上底长为8厘米，下底长为12厘米，那么它的高h = 2*60/(8+12) = 6厘米。

需要注意的是，在使用此公式时，必须确保已知梯形的面积和上下底长。如果缺少其中任何一个数据，就无法直接使用此公式求高。这种方法简单直接，适用于已知梯形面积和上下底长的场景。但如果缺少这三个量中的一个，则需采取其他的计算方法。

已知梯形周长、对角线和角度求高

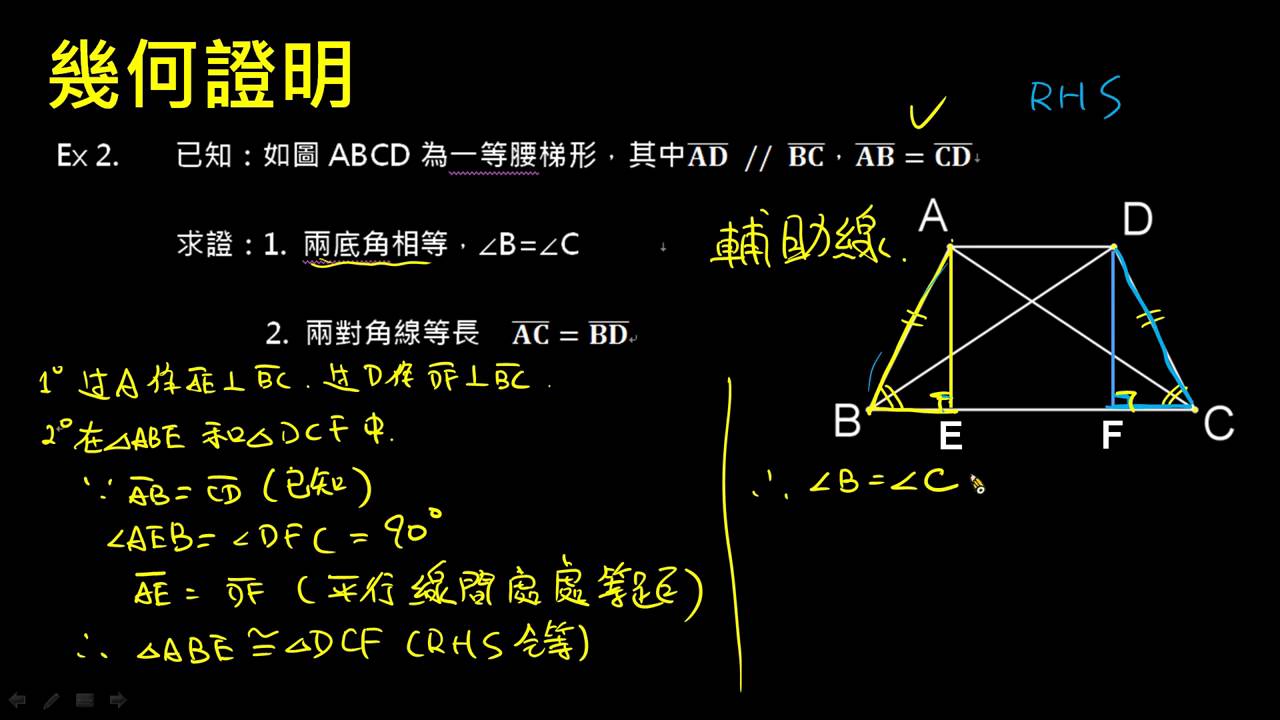
当我们只知道梯形的周长、对角线长度及相关角度时，可以运用三角函数知识求解梯形的高。设梯形ABCD中，AB为上底，CD为下底，AC和BD为对角线，已知周长为P，对角线AC=m，BD=n。根据勾股定理和三角函数关系，我们可以列出方程组求解高。例如，如果梯形为等腰梯形，那么我们可以通过作高，将梯形分解成矩形和两个直角三角形，利用三角函数关系求出高。

例如，已知等腰梯形上底为4，下底为8，对角线为5，我们可以通过勾股定理及三角函数关系来求高。然而，此方法的计算过程相对复杂，需要一定的数学基础。

此外，在实际应用中，准确测量梯形的周长、对角线长度及角度并不容易，这也会影响计算结果的精度。

利用坐标法求梯形的高

如果梯形的四个顶点坐标已知，那么我们可以利用坐标法求出梯形的高。首先，我们需要找到梯形的两条平行边（上下底）。然后，我们可以利用两点间的距离公式计算出上下底的长度，以及两条平行边之间的垂直距离，这个垂直距离就是梯形的高。

例如，已知梯形ABCD的坐标分别为A(1,1)，B(5,1)，C(4,4)，D(2,4)。我们可以计算出AB和CD的长度分别为4和2，通过两点间的距离公式和斜率公式，计算出高。

该方法的优点是精确，且不受梯形形状限制，适用于各种梯形。其缺点是需要事先知道梯形顶点的坐标信息。

特殊梯形的求高方法

对于一些特殊类型的梯形，例如等腰梯形、直角梯形，我们可以利用其特殊性质简化求高过程。

等腰梯形：等腰梯形具有对称性，我们可以通过作高线，将等腰梯形分成两个全等的直角三角形和一个矩形，利用勾股定理或三角函数求高。

直角梯形：直角梯形有一条直角边作为高，因此求高比较简单，直接测量或计算直角边即可。

这些特殊性质使得计算更为简便。但在实际应用中，并非所有梯形都属于特殊类型。

总结与展望

综上所述，求梯形的高有多种方法，选择哪种方法取决于已知条件。如果已知梯形的面积和上下底，则可以直接利用面积公式求高；如果已知梯形的周长、对角线及角度，则需要运用三角函数进行计算；如果已知梯形的顶点坐标，则可利用坐标法求高；对于特殊梯形，可以利用其特殊性质简化求高过程。

未来，随着计算机技术和算法的发展，求解梯形的高将会更加便捷和高效。例如，利用计算机辅助设计软件，我们可以直接输入梯形的相关参数，软件会自动计算出梯形的高。