梯形的下底怎么求？详解梯形下底计算方法及应用场景

本文系统地讲解了如何计算梯形的下底，涵盖了多种已知条件下的计算方法和实际应用场景。文章强调了在计算过程中需要注意的误区和注意事项，并对梯形下底计算的未来发展趋势进行了展望，旨在帮助读者全面掌握梯形下底的计算技巧，提升解决实际问题的效率。文章中提到的“已知面积求下底”和“梯形下底多种求解方法”是解决问题的关键，也是本文的核心内容。

梯形下底计算公式及推导

梯形的下底计算方法取决于已知条件的不同。最基本的公式是基于梯形的面积公式推导出来的。梯形的面积S = (上底a + 下底b)h/2，其中a为上底，b为下底，h为高。

如果已知梯形的面积S、上底a和高h，则我们可以通过变形公式求出下底b：b = 2S/h - a。

例如，一个梯形的面积是30平方厘米，上底是4厘米，高是5厘米，那么下底b = (2 * 30)/5 - 4 = 8厘米。这个公式简洁明了，是求梯形下底最常用的方法。

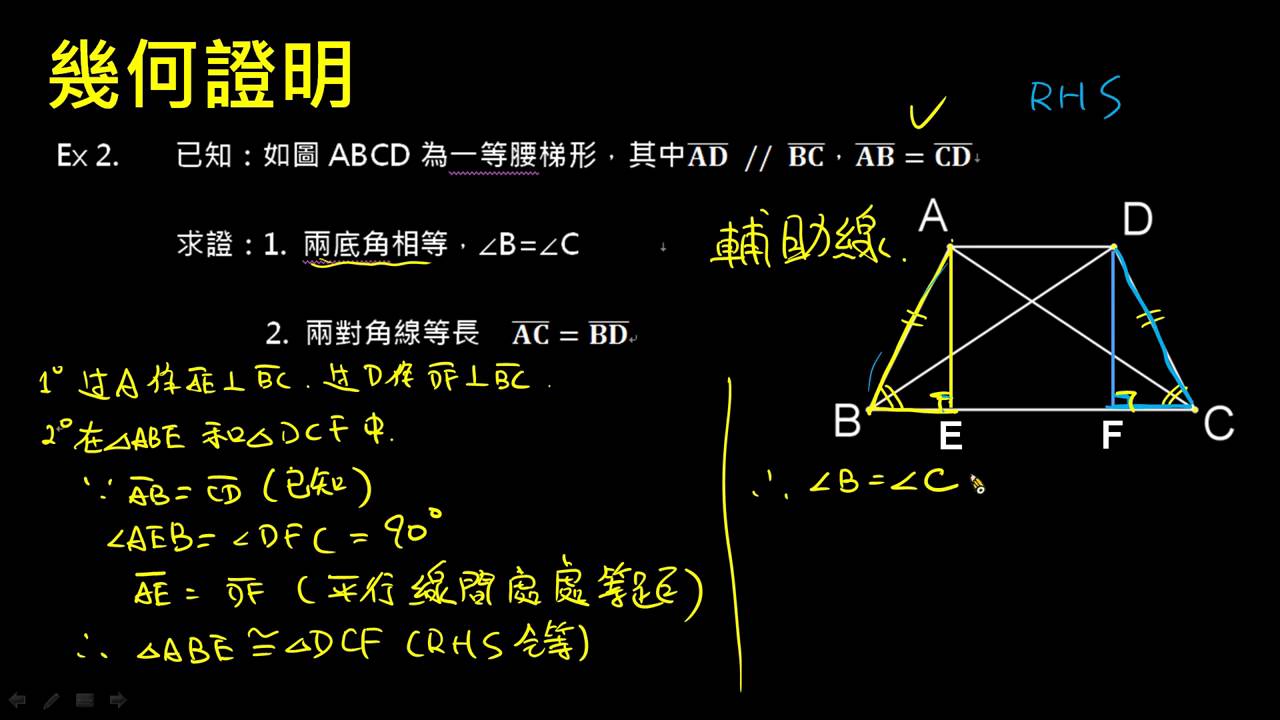
此外，在一些特殊情况下，例如等腰梯形，我们可以利用勾股定理等几何知识，结合已知的边长和角度来计算下底。不同的条件下，需要灵活运用不同的几何知识进行求解。

需要注意的是，在实际应用中，我们需要根据实际情况选择合适的公式，并保证数据的准确性，才能得到正确的结果。任何微小的误差都可能导致最终结果的偏差。

不同已知条件下梯形下底的求解方法

除了已知面积、上底和高的情况，还有其他几种情况需要我们掌握不同的求解方法。

例如，如果已知梯形的两条腰长、上底和高，我们可以利用勾股定理来求解下底。

再例如，如果已知梯形的四个顶点坐标，我们可以利用坐标系中的距离公式计算上底、下底和高，进而得到梯形的面积和下底长度。

还有一种情况，如果已知梯形的周长、上底和高，可以先利用周长求出腰长，再利用勾股定理求出下底。总之，面对不同条件，我们应该灵活运用各种数学方法和公式进行求解，并认真检查计算结果，确保计算的精确度。

需要强调的是，对于复杂的梯形问题，我们需要结合图形分析，找出已知条件与未知条件之间的关系，从而建立方程组进行求解。对于较为复杂的几何问题，建议结合绘图工具辅助理解和求解。

梯形下底计算在实际生活中的应用

• 土木工程中的应用：在计算土方工程量、桥梁设计等方面，梯形下底的计算至关重要。例如，计算渠道的过水面积，需用到梯形的面积公式。
• 农业生产中的应用：例如计算梯田的面积，以确定播种量和施肥量。不同梯田的面积不同，需要计算各个梯田的面积，才能合理安排农业生产。
• 建筑设计中的应用：建筑物的外形设计中，经常会出现梯形结构，需要计算梯形下底来确定建筑材料的用量和成本。比如，斜屋顶的面积计算。
• 地图测绘中的应用：在进行地形测绘时，常需要计算梯形面积，例如计算山坡面积，或是不规则地块面积的近似计算。
• 其他应用：在日常生活中，我们也可能会遇到需要计算梯形下底的情况，例如计算不规则图形的面积，以确定材料的用量等。

梯形下底计算的误区及注意事项

在计算梯形的下底时，一些常见的误区需要注意避免。

首先，要明确梯形的定义和相关概念，例如上底、下底、高、腰等。

其次，要根据已知条件选择正确的计算公式，避免公式使用错误。

再次，计算过程中要注意单位换算，避免因单位不一致导致计算结果错误。例如，面积单位是平方米，高和底的单位是米。

最后，计算结果需要进行检验，确保结果的合理性和准确性。可以使用不同方法进行验证。

一些同学可能会混淆梯形和其他的四边形，例如平行四边形，从而导致计算错误。需要仔细辨别图形的特性。

对于较为复杂的几何问题，需要认真分析题意，准确地提取信息，利用几何知识建立方程组并解出最终答案。

总之，准确理解梯形的性质和公式是解决问题的关键。

总结与展望

本文详细介绍了梯形下底的多种计算方法，并分析了其在实际生活中的应用以及计算过程中需要注意的误区。掌握梯形下底的计算方法，不仅对于解决数学问题至关重要，也能够帮助我们更好地理解和解决现实生活中的实际问题。

未来，随着科技的不断发展，计算工具和方法也会不断完善，这将使梯形下底的计算更加便捷和高效。例如，一些数学软件可以帮助我们快速计算复杂的梯形问题。

同时，我们也可以借助计算机辅助设计软件（CAD）进行图形绘制和计算。这些工具可以帮助我们更直观地理解梯形的性质和计算过程，提高计算效率，并减少错误的可能性。