正方体的表面积怎么求？详解计算方法及应用场景

本文详细阐述了正方体的表面积计算方法，从公式推导到实际应用，再到常见错误及未来发展趋势，进行了全面的探讨。通过学习正方体表面积的计算方法，以及理解正方体展开图面积计算，我们能够更好地解决实际问题，例如包装盒的设计和建筑工程中的面积计算等。

正方体表面积计算公式及推导

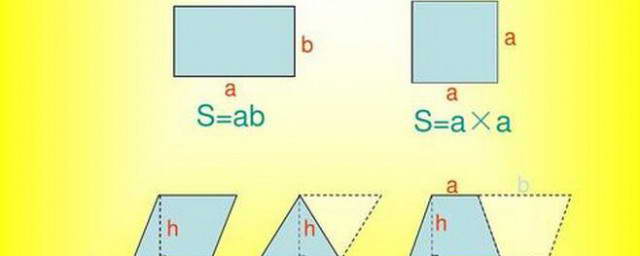
正方体的表面积是指构成正方体六个面的总面积。由于正方体的六个面都是全等的正方形，因此计算其表面积的关键在于先求出单个正方形的面积，再乘以6。

假设正方体的边长为a，则单个正方形的面积为a²。那么，正方体的总表面积S就可以表示为：S = 6a²。

这个公式的推导非常直观：正方体有6个面，每个面都是边长为a的正方形，面积为a²，所以总面积是6个a²的和。

我们可以通过一个简单的例子来理解：假设一个正方体的边长为5厘米，那么它的表面积就是6 × 5² = 150平方厘米。

理解这个公式的关键在于理解正方体的几何特性，以及面积计算的基本原理。很多几何问题的解决都依赖于对基本公式和概念的掌握。

不同场景下正方体表面积的应用

正方体表面积的计算并非仅仅是数学课本上的一个公式，它在现实生活中有着广泛的应用。例如，在包装设计中，我们需要计算包装盒的用料面积，这时正方体表面积的计算就显得尤为重要。

假设我们要设计一个边长为10厘米的正方体礼品盒，那么我们需要至少准备6 × 10² = 600平方厘米的包装材料。这需要考虑材料的损耗，以及盒子的粘合部分。实际应用中，我们还需要考虑包装盒的结构，这可能会增加材料的使用量。

另一个例子是建筑工程中，计算建筑物外墙的面积。如果建筑物的一部分是正方体结构，那么我们可以运用正方体表面积的计算来估算外墙的面积，从而计算所需的涂料或瓷砖数量。这个计算可以帮助我们更好地规划工程预算和材料采购。

正方体表面积计算中的常见错误及解决方法

• 忽略单位：计算表面积时一定要注意单位的一致性，例如，边长是厘米，则表面积的单位是平方厘米。
• 公式混淆：将正方体的表面积公式与体积公式混淆。正方体体积公式是V = a³。
• 计算错误：在计算a²或6a²时出现简单的算术错误。
• 维度理解错误：没有理解平方厘米等面积单位的含义。
• 忽略实际应用中的损耗：在实际应用中，需要考虑到材料的损耗等实际因素。

正方体表面积计算的未来发展与挑战

随着科技的发展，正方体表面积的计算方法也可能会有新的发展。例如，可以利用计算机辅助设计（CAD）软件，更精确地计算不规则形状的表面积，即使其中包含正方体结构的部分。

未来的挑战在于如何更有效地计算更复杂形状的表面积，比如一些不规则的几何体，它们可能包含正方体、长方体等多种几何形状。这需要更先进的算法和更强大的计算能力。

此外，在一些特殊情况下，比如在微观尺度上，传统的计算方法可能需要修正。因此，未来需要更深入的研究，以完善和改进正方体的表面积计算方法，以适应更广泛的应用场景。

同时，随着三维打印技术的发展，对复杂形状的表面积计算需求不断增加，这将推动相关算法和软件的进一步发展。