圆锥的表面积怎么求？全面解析计算公式及应用场景

本文深入探讨了圆锥的表面积计算方法，从公式推导到实际应用，并分析了其局限性和未来发展趋势。文章详细讲解了圆锥侧面积和全面积的计算公式，并通过多个案例分析，帮助读者掌握不同类型圆锥表面积的求解技巧。此外，文章还探讨了圆锥表面积计算在不同领域中的应用，以及未来发展趋势。了解如何计算圆锥的表面积，对于工程技术人员、设计师以及数学爱好者都具有重要意义。

圆锥表面积计算公式的推导与理解

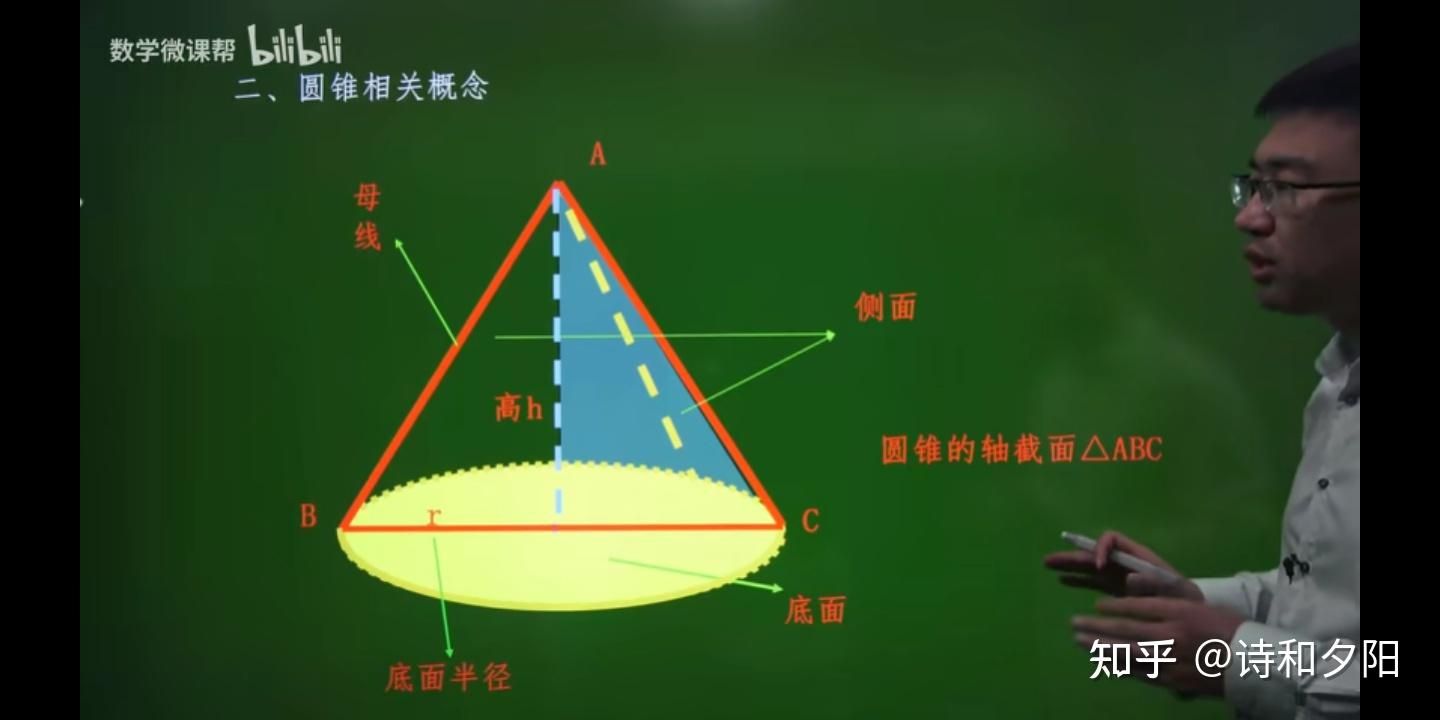
求圆锥的表面积，首先要明确圆锥的结构。圆锥由一个底面和一个侧面构成，底面是一个圆形，侧面是一个曲面。因此，圆锥的表面积等于其侧面积与底面积之和。

计算圆锥侧面积的关键在于理解其展开图。将圆锥的侧面展开，会得到一个扇形。这个扇形的弧长等于圆锥底面的周长，而扇形的半径等于圆锥的母线长。利用扇形的面积公式，我们可以推导出圆锥侧面积的计算公式：S侧 = πrl，其中r为圆锥底面半径，l为圆锥母线长。

底面积的计算则相对简单，直接套用圆的面积公式即可：S底 = πr²。

因此，圆锥的全面积公式为：S全 = S侧 + S底 = πrl + πr² = πr(l+r)。

理解公式推导过程，有助于我们更好地应用公式。例如，如果已知圆锥的底面半径和高，我们可以利用勾股定理计算出母线长l，进而计算出圆锥的表面积。在实际应用中，我们经常会遇到已知部分条件求解表面积的情况，这就需要我们灵活运用公式进行变形和计算。

不同类型圆锥表面积计算的案例分析

掌握圆锥表面积的计算公式只是第一步，更重要的是能够灵活运用公式解决实际问题。

例如，一个圆锥形沙堆，底面半径为 2 米，母线长为 3 米，那么它的表面积是多少？我们可以直接套用公式 S全 = πr(l+r) = π * 2 * (3+2) = 10π 平方米。

如果已知圆锥的高 h 和底面半径 r，则需先计算母线长 l = √(r²+h²) ，然后代入全面积公式。

再比如，一个圆锥形容器，底面直径为 10cm，高为 12cm，求其内表面积。这里需要根据容器的实际情况选择计算公式，考虑是否需要计算底面积。一些特殊的圆锥形物体，比如圆台，其表面积计算则需要将圆台分解成圆锥和圆柱进行分别计算再求和。

通过以上案例分析，我们可以看到，掌握圆锥表面积计算方法的关键在于准确理解题意，选择合适的公式，并进行准确的计算。

圆锥表面积计算公式的应用及局限性

圆锥表面积的计算公式在诸多领域都有广泛的应用，例如工程建设、包装设计、工业制造等。在工程建设中，计算圆锥形建筑物的表面积，可以帮助我们准确估算所需材料的数量，降低成本。在包装设计中，计算圆锥形包装的表面积，可以帮助我们优化包装材料的利用率，提高效率。在工业制造中，计算圆锥形零件的表面积，可以帮助我们提高生产精度，保证产品质量。

然而，圆锥表面积的计算公式也存在一定的局限性。首先，该公式只适用于规则的圆锥，对于不规则的圆锥，则需要采用其他方法进行计算。其次，该公式的计算结果是理论值，实际值可能会因为各种因素的影响而存在偏差。例如，在测量圆锥的底面半径和母线长时，可能会存在误差。

因此，在应用圆锥表面积的计算公式时，我们需要根据实际情况进行调整，并对计算结果进行合理的分析和判断。在工程应用中，我们需要考虑安全系数等因素。

圆锥表面积计算在未来发展趋势的探讨

随着科技的进步，圆锥表面积的计算方法也在不断发展。例如，计算机技术的应用，使得我们可以利用计算机软件进行复杂的圆锥表面积计算，提高计算精度和效率。此外，三维建模技术的应用，使得我们可以更加直观地观察圆锥的表面积，并进行更精确的测量。

未来，随着人工智能和机器学习技术的不断发展，可能会出现更智能化的圆锥表面积计算方法，例如自动识别不规则圆锥，并进行精确计算。同时，虚拟现实和增强现实技术的应用，也可能会为圆锥表面积的计算提供新的思路和方法。

但我们也要看到，圆锥表面积计算方法的发展仍然面临着一些挑战，例如如何提高计算精度和效率，如何处理不规则圆锥，如何减少计算误差等。只有不断攻克这些挑战，才能使圆锥表面积的计算方法更好地服务于各个领域。