直角三角形斜边长度怎么算？勾股定理及应用详解

本文深入浅出地讲解了如何计算直角三角形斜边长度，从勾股定理的基本原理到实际应用，以及其局限性与挑战，并从不同角度进行了深入的分析。文章还介绍了利用勾股定理计算斜边的步骤，并结合实际案例，帮助读者更好地理解和应用相关知识，例如如何利用直角三角形斜边计算公式和直角三角形斜边计算器来解决问题。

勾股定理：直角三角形斜边长度计算的基石

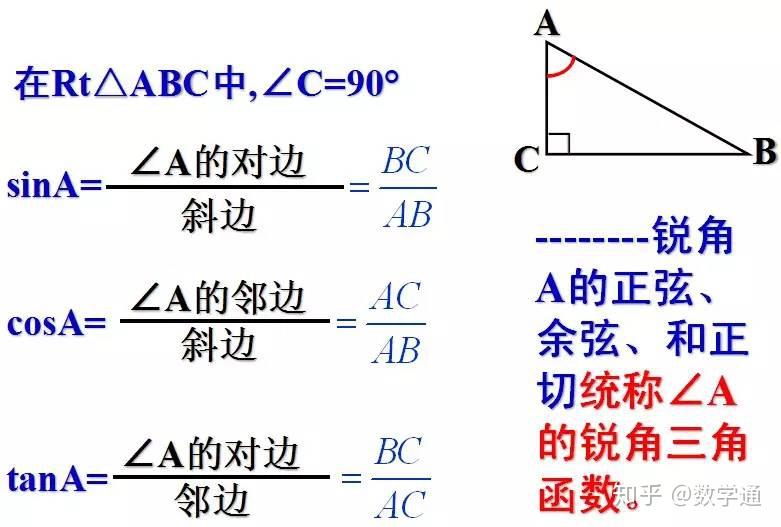
计算直角三角形斜边长度最基础的方法，就是运用著名的勾股定理。勾股定理，又称毕达哥拉斯定理，它指出在直角三角形中，两条直角边的平方和等于斜边的平方。用公式表示就是：a² + b² = c²，其中a和b分别代表直角三角形的两条直角边长度，c代表斜边长度。

理解勾股定理的关键在于明白它描述的是直角三角形三边之间的一种特殊关系。这个关系在几何学和许多实际应用中都至关重要。例如，我们可以利用勾股定理计算建筑物的高度、测量土地面积、规划道路等。

历史上，勾股定理的发现和证明过程是一个漫长的过程，许多古代文明都独立地发现了这个定理的不同形式。中国古代的《周髀算经》中就记载了勾股定理及其应用。而古希腊数学家毕达哥拉斯则被广泛认为是第一个给出勾股定理证明的人，因此定理也以他的名字命名。

学习勾股定理时，不仅要记住公式，更要理解其背后的几何意义。这有助于我们更灵活地运用勾股定理解决各种问题。

直角三角形斜边长度计算的实际应用

勾股定理并非仅仅是数学理论，它在现实生活中有着广泛的应用。例如，在土木工程中，工程师们经常利用勾股定理计算建筑物的高度、桥梁的跨度以及其他结构的尺寸。

在测量学中，勾股定理也扮演着重要的角色。例如，测量员可以利用勾股定理计算两点之间的距离，或者测量土地的面积。

此外，在导航领域，勾股定理也可以用来计算航海或航空中的距离。例如，飞机飞行员可以利用勾股定理计算飞机与目的地之间的距离，并规划最佳飞行路线。

甚至在日常生活中，我们也会不自觉地运用勾股定理的思想。例如，我们需要确定电视屏幕的对角线长度，实际上就是应用了勾股定理的原理。

总而言之，勾股定理是解决直角三角形斜边长度计算的关键，其应用广泛且深入到生活的各个方面。

利用勾股定理计算斜边长度的步骤

• 首先，明确已知条件：直角三角形的两条直角边长度。
• 其次，根据勾股定理公式：a² + b² = c²，将已知条件代入公式中。
• 再次，进行计算：计算a² 和b²，然后将两者相加得到c²。
• 然后，开平方：对c²进行开平方运算，得到斜边长度c。
• 最后，检查结果：检查计算结果是否合理，确保斜边长度大于两条直角边长度。
• 根据实际情况选择合适的计算工具，例如计算器或者专业的计算软件。
• 注意单位换算：确保所有数据都使用相同的单位，例如米或厘米，避免单位换算错误。

直角三角形斜边长度计算的局限性与挑战

虽然勾股定理为计算直角三角形斜边长度提供了简单有效的方法，但它也存在一定的局限性。首先，勾股定理只适用于直角三角形，对于其他类型的三角形，我们需要使用其他的三角函数公式进行计算。

其次，在实际应用中，由于测量误差的存在，计算结果可能存在一定的偏差。因此，我们需要采用更精确的测量工具和方法，以提高计算结果的准确性。

此外，对于一些复杂的几何问题，我们可能需要结合其他几何知识以及多种方法来求解斜边长度，例如涉及多个直角三角形的组合问题。

未来，随着科技的发展，一些新的技术和方法可能会对直角三角形斜边长度的计算带来新的突破，例如更精确的传感器技术和更强大的计算能力，这些技术可以帮助我们更精确、更快速地进行计算，提高效率，并解决一些目前难以解决的问题。

不同角度理解直角三角形斜边长度计算

理解直角三角形斜边长度计算，不应仅仅停留在勾股定理公式的表面，更要从不同的角度深入理解。例如，从几何角度，勾股定理体现了直角三角形三边之间的内在关系；从代数角度，它是一个二元二次方程的解；从物理角度，它可以用于解决力学、运动学等问题。

此外，我们还可以从历史的角度看待勾股定理，了解其发现和证明的过程，以及它对数学发展的重要意义。从应用的角度来看，理解勾股定理的广泛应用，可以帮助我们解决现实生活中的实际问题。

对于初学者来说，理解勾股定理的核心是掌握其基本原理和计算方法；对于进阶学习者来说，则需要更深入地探究其本质和应用，并尝试将它与其他数学知识结合起来解决更复杂的问题。