本文详细阐述了平方是怎么算,从基本概念到不同类型数字的计算技巧,再到其在生活中的应用和未来发展趋势。文章深入浅出地讲解了平方计算方法,并结合实际案例分析了其应用,希望帮助读者轻松掌握平方运算,并对平方计算在未来的发展有更清晰的认识。文章中提到的长尾关键词包括整数平方计算技巧,小数平方计算技巧以及平方在面积计算中的应用等,为读者提供了更全面的学习资源。
平方计算的基本概念与方法
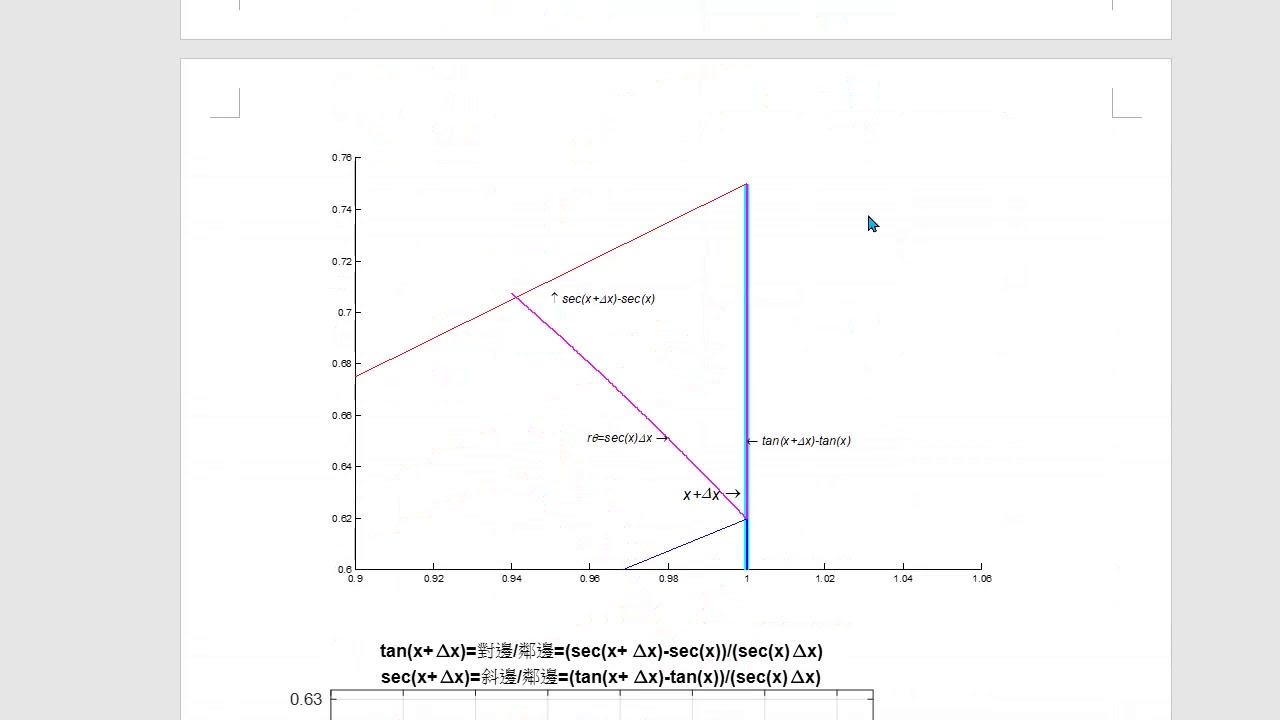
平方,简单来说,就是一个数乘以它本身的结果。例如,5 的平方就是 5 × 5 = 25,记作 5²。这个小小的算术运算,在数学、物理、工程等众多领域都有着广泛的应用。
理解平方计算的关键在于掌握乘法运算。对于简单的整数,直接进行乘法计算即可。例如,计算 12 的平方,直接计算 12 × 12 = 144。
然而,对于较大的整数、小数甚至分数,直接计算可能较为繁琐。这时,可以利用一些辅助工具,例如计算器,或者运用一些简便的计算方法,如公式法等。例如,计算 1.5 的平方,可以利用(a+b)²=a²+2ab+b² 的公式,将 1.5 看作 1+0.5,则 1.5² = (1+0.5)² = 1² + 2 × 1 × 0.5 + 0.5² = 1 + 1 + 0.25 = 2.25。
对于一些特殊的数,例如 10 的倍数,计算平方也会有一些技巧。例如,计算 20 的平方,可以先计算 2 的平方,即 4,然后在结果后面加上两个 0,得到 400。这种方法简化了计算过程,提高了效率。
不同类型数字的平方计算技巧
掌握了平方计算的基本方法后,我们还可以针对不同类型的数字,学习一些相应的技巧,以提高计算效率。
对于整数的平方计算,我们可以利用一些规律。例如,一个数的个位数是 5 的整数,其平方的个位数一定是 25,十位数可以根据十位数计算得到,例如 15²=225,25²=625。
小数的平方计算,可以利用 (a+b)²=a²+2ab+b²的公式进行展开计算,或者将小数转换为分数后再进行计算。例如 0.8² = (8/10)²= 64/100 = 0.64,又例如 0.12² = (12/100)²=144/10000=0.0144。
分数的平方计算,可以先计算分子和分母的平方,然后将结果约分。例如,(2/3)² = (2²)/(3²) = 4/9。
熟练掌握这些技巧,可以使平方计算更加简便快捷。
平方在日常生活中的实际应用
平方计算并非仅仅局限于数学课堂,它在日常生活中也有着广泛的应用。
例如,在计算面积时,经常会用到平方。例如,计算一个正方形的面积,需要将边长进行平方运算。一个边长为 5 米的正方形,它的面积就是 5² = 25 平方米。
在工程建设中,平方计算也扮演着重要的角色。例如,计算地砖的铺设面积,或者计算房屋的占地面积,都需要用到平方计算。
此外,平方计算还广泛应用于物理学、工程学等领域。例如,计算速度、能量、功率等物理量,都可能涉及到平方运算。
在日常生活中,我们可能意识不到,但其实我们经常在运用平方计算,理解平方计算可以更好地帮助我们解决生活中的实际问题。
平方计算的未来发展趋势及挑战
随着科技的进步,平方计算的方法和应用领域也在不断发展。未来,可能会有更加高效、便捷的平方计算方法被开发出来,例如人工智能辅助计算,以进一步提升计算效率和精度。
另一方面,随着大数据时代的到来,对海量数据的处理和分析提出了新的挑战。如何快速、准确地进行大量的平方运算,是需要解决的一个关键问题。 这就需要更强大的计算工具和更有效的算法来支持。
此外,在教育领域,如何更好地引导学生理解平方计算的概念,并掌握相关的计算技巧,也是一个重要的课题。 这需要开发更有效的教学方法和教学工具。
总之,平方计算虽然是一个简单的数学运算,但它却在我们的生活中扮演着重要的角色,并且其发展与技术的进步密切相关。






 鄂ICP备15020274号-1
鄂ICP备15020274号-1