等腰三角形斜边计算方法详解：不同情况下的解题技巧与应用

本文深入探讨了等腰三角形斜边计算方法，涵盖了直角等腰三角形和非直角等腰三角形的计算技巧。通过分析不同情况下的解题方法，以及实际应用案例和常见误区，帮助读者全面掌握等腰三角形斜边计算。文章还展望了该计算方法的未来发展趋势，包括运用计算机辅助设计软件、三维建模技术等，进一步提升计算效率和精度。

直角等腰三角形的斜边计算

直角等腰三角形是等腰三角形的一种特殊情况，它的一条直角边与另一条直角边长度相等，两条直角边长度等于斜边的√2倍。

例如，已知直角等腰三角形的直角边长为a，根据勾股定理，斜边c可以表示为c = √(a² + a²) = a√2。这个公式非常简单易懂，只需要知道直角边长度就能快速计算出斜边。

在实际应用中，直角等腰三角形经常出现在工程测量和建筑设计中。例如，计算屋顶斜梁长度、设计正方形的斜对角线长度等都离不开直角等腰三角形的斜边计算。

根据我国建筑规范，一些建筑结构的设计需要用到直角等腰三角形，这要求设计人员必须能够准确计算斜边长度，从而保证建筑的稳定性和安全性。不正确的计算可能会导致建筑物结构不稳定，甚至发生坍塌事故。

因此，熟练掌握直角等腰三角形斜边计算对于相关专业人士至关重要。

非直角等腰三角形的斜边计算

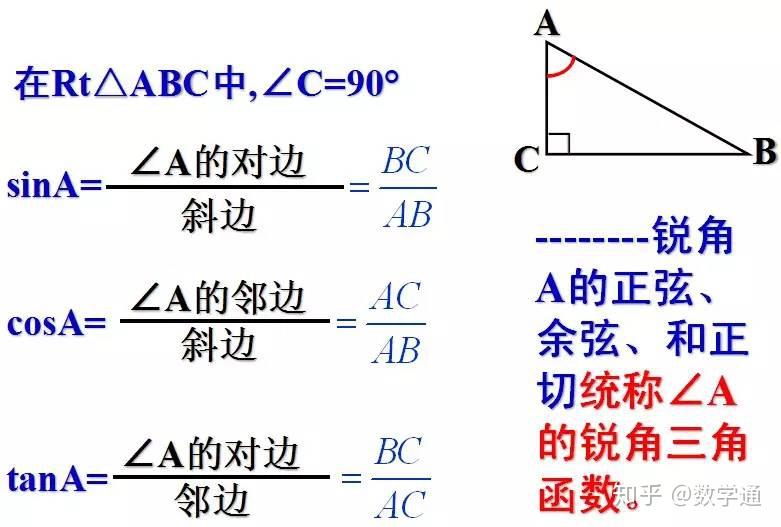
对于非直角等腰三角形，计算斜边需要运用三角函数或余弦定理。

如果已知等腰三角形的腰长a和顶角θ，那么根据余弦定理，斜边c可以表示为：c² = a² + a² - 2a²cosθ = 2a²(1-cosθ)，因此c = a√[2(1-cosθ)]。

如果已知等腰三角形的腰长a和底边b，那么可以使用勾股定理的变形公式进行计算。假设从顶点向底边作垂线，将三角形分成两个直角三角形。设垂线长度为h，则h² + (b/2)² = a²，求出h后，再利用勾股定理计算斜边，但这方法略显繁琐。

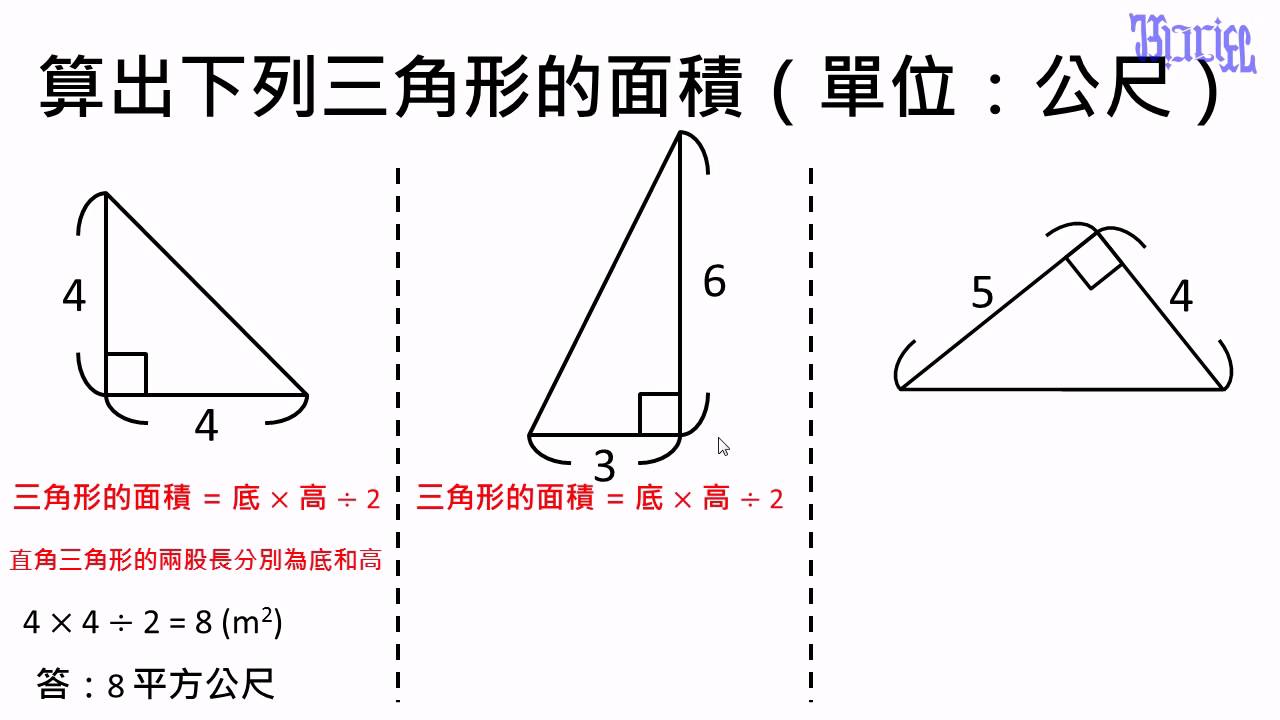
以一个等腰三角形为例，腰长为 5cm，底边为 6cm。先计算高：h² = 5² - (6/2)² = 16, h = 4cm。然后利用勾股定理，其中一边是高h，另一边是底边的一半，斜边c = √(4² + 3²) = 5cm。这与已知的腰长一致。

这说明对于非直角等腰三角形，根据已知条件选择合适的公式至关重要。

等腰三角形斜边计算的实际应用及误区

等腰三角形斜边计算在现实生活中有着广泛的应用，例如：

1. 土木工程：桥梁、建筑物的设计与施工中，常需计算斜撑、屋架等结构的长度，这都离不开等腰三角形斜边的计算。

2. 测量学：测算距离、高度等，常利用等腰三角形的特性，通过斜边计算来间接求解。

3. 航空航天：飞机机翼的设计、导弹轨迹的计算等都涉及到等腰三角形斜边计算。

然而，在实际应用中，一些常见的误区需要特别注意：

1. 混淆直角等腰三角形与非直角等腰三角形的计算方法。

2. 数据单位不统一，导致计算结果错误。

3. 忽略计算过程中的细节，导致计算出错。

准确的计算需要严谨的步骤和细致的检查。

等腰三角形斜边计算方法的拓展与发展

• 运用计算机辅助设计软件进行计算，提高计算效率和精度。
• 结合三维建模技术，更直观地展示和分析等腰三角形斜边计算结果。
• 探索更简便、更精确的计算方法，例如结合现代数学工具进行研究。
• 将等腰三角形斜边计算与其他几何知识结合起来，进行更深入的学习和研究。
• 将等腰三角形斜边计算应用于更多领域，例如人工智能、大数据等。